
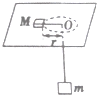
 如图所示,细绳的一端系着质量为M=2kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5kg,M的中点与圆孔的距离为0.5m,并已知M与圆盘的最大静摩擦力为4N,现使此圆盘绕中心轴线转动,则物体的角速度ω取以下值可使m处于静止状态,(g取10m/s2)( )
如图所示,细绳的一端系着质量为M=2kg的物体,静止在水平圆盘上,另一端通过光滑的小孔吊着质量为m=0.5kg,M的中点与圆孔的距离为0.5m,并已知M与圆盘的最大静摩擦力为4N,现使此圆盘绕中心轴线转动,则物体的角速度ω取以下值可使m处于静止状态,(g取10m/s2)( )| A. | ω=1.5 rad/s | B. | ω=2 rad/s | C. | ω=0.8 rad/s | D. | ω=3 rad/s |
分析 当此平面绕中心轴线以角速度ω转动时,若M恰好要向里滑动时,ω取得最小值,此时M所受的静摩擦力达到最大,方向沿半径向外,由最大静摩擦力和绳子拉力的合力提供M所需要的向心力.若M恰好要向外滑动时,ω取得最大值,此时M所受的静摩擦力达到最大,方向沿半径向里,由最大静摩擦力和绳子拉力的合力提供M所需要的向心力.根据牛顿第二定律分别求出ω的最小值和最大值,即可得到ω的取值范围.
解答 解:当物体M在此平面绕中心轴线以ω角速度转动时,当M恰好要向里滑动时,ω取得最小值为ωmin,此时M所受的静摩擦力达到最大为Fmax,方向沿半径向外,由最大静摩擦力和绳子拉力的合力提供所需要的向心力,根据牛顿第二定律和向心力公式有:mg-Fmax=Mωmin2r,代入数据解得ωmin=1 rad/s.
当M恰好要向外滑动时,ω取得最大值为ωmax,此时M所受的静摩擦力达到最大为Fmax,方向沿半径向里,由最大静摩擦力和绳子拉力的合力提供所需要的向心力,根据牛顿第二定律和向心力公式有:mg+Fmax=Mωmax2r,代入数据解得ωmax=3 rad/s.
所以角速度的取值范围是 1 rad/s≤ω≤3 rad/s,可使m处于静止状态,所以选项ABD正确,C错误.
故选:ABD
点评 本题是圆周运动中临界问题,抓住当M恰好相对此平面刚要滑动时静摩擦力达到最大,由牛顿第二定律求解角速度的取值范围


科目:高中物理 来源: 题型:选择题
| A. | 位移为零时,路程一定为零 | |
| B. | 路程一定大于位移 | |
| C. | 物体沿曲线运动时,位移的大小可能大于路程 | |
| D. | 物体沿直线单方向运动时,位移的大小一定等于路程 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

| 电压表V1读数U1(V) | 1.88 | 1.92 | 1.94 | 1.98 | 2.00 |
| 电压表V2读数U2(V) | 1.72 | 1.25 | 1.00 | 0.60 | 0.34 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题
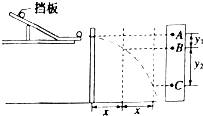 “研究平抛运动”的实验装置如图所示,实验步骤如下:
“研究平抛运动”的实验装置如图所示,实验步骤如下:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
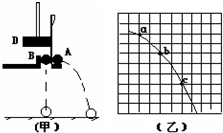 在“探究平抛运动的规律”的实验中,分成两步进行:
在“探究平抛运动的规律”的实验中,分成两步进行:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
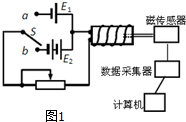
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | r=$\frac{T}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$ | B. | r=$\frac{T}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π{r}_{1}}\sqrt{\frac{Gm}{{r}_{1}}}$ | ||
| C. | r=$\frac{2π}{T}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π}\sqrt{\frac{Gm}{{r}_{1}}}$ | D. | r=$\frac{2π}{T}\sqrt{\frac{Gm}{{r}_{1}}}$,M=$\frac{mT}{2π{r}_{1}}\sqrt{\frac{Gm}{{r}_{1}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 甲、乙两汽车之间的距离一定不断减小 | |
| B. | 甲、乙两汽车之间的距离可能先不断减小、后不断增大 | |
| C. | 若v>$\sqrt{2({a}_{1}+{a}_{2})d}$,则两汽车一定不会相撞 | |
| D. | 若v<$\sqrt{2({a}_{1}+{a}_{2})d}$,则两汽车一定不会相撞 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com