
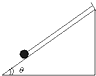
 一个质量为0.2kg的小球用细线吊在倾角θ=53°的斜面顶端,如图,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10m/s2的加速度向右做加速运动时,则( )(sin53°=0.8,cos53°=0.6,g=10m/s2 )
一个质量为0.2kg的小球用细线吊在倾角θ=53°的斜面顶端,如图,斜面静止时,球紧靠在斜面上,绳与斜面平行,不计摩擦,当斜面以10m/s2的加速度向右做加速运动时,则( )(sin53°=0.8,cos53°=0.6,g=10m/s2 )| A. | 绳的拉力为1.60N | B. | 绳的拉力为2$\sqrt{2}$N | ||
| C. | 斜面对小球的弹力为1.20N | D. | 斜面对小球的弹力为0 |
分析 首先判断小球是否飞离了斜面,根据小球刚刚飞离斜面的临界条件,即绳子的倾角不变,斜面的支持力刚好为零,解出此时的加速度与题目给出的加速度大小进行比较,若给出加速度大于小球的临界加速度说明小球已经飞离了斜面,否则小球还在斜面上.
解答  解:当加速度a较小时,小球与斜面一起运动,此时小球受重力、绳子拉力和斜面的支持力,绳子平行于斜面;当加速度a足够大时,小球将飞离斜面,此时小球仅受重力与绳子的拉力作用,绳子与水平方向的夹角未知,而题目要求出当斜面以10m/s2的加速度向右做加速运动时,绳的拉力及斜面对小球的弹力,必须先求出小球离开斜面的临界加速度a0,(此时小球所受斜面的支持力恰好为零)
解:当加速度a较小时,小球与斜面一起运动,此时小球受重力、绳子拉力和斜面的支持力,绳子平行于斜面;当加速度a足够大时,小球将飞离斜面,此时小球仅受重力与绳子的拉力作用,绳子与水平方向的夹角未知,而题目要求出当斜面以10m/s2的加速度向右做加速运动时,绳的拉力及斜面对小球的弹力,必须先求出小球离开斜面的临界加速度a0,(此时小球所受斜面的支持力恰好为零)
小球的受力如图:
由牛顿第二定律得:F合=mgcotθ=ma0
解得:a0=gcotθ=7.5m/s2
因为:a=10m/s2>a0
所以小球一定离开斜面N=0,小球的受力如图所示:
则水平方向有牛顿第二定律得:Tcosα=ma
竖直方向有受力平衡得:Tsinα=mg
由以上两式整理得:T=$\sqrt{(ma)^{2}+(mg)^{2}}$=$\sqrt{2×4}$=2$\sqrt{2}$N;
N=0
故选:BD.
点评 此题最难解决的问题是小球是否飞离了斜面,我们可以用假设法判断出临界加速度来进行比较;所以本题应首先利用临界问题分析小球是否漂浮.


科目:高中物理 来源: 题型:选择题
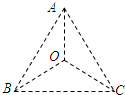 如图所示,在真空中等边三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q,此时三角形中心O处场强大小为E,电势为U,选无穷远处电势为零,现将A处的-Q换成+Q,其他条件不变,则中心O处场强大小和电势分别为( )
如图所示,在真空中等边三角形三个顶点A、B、C处分别固定点电荷-Q、+Q、+Q,此时三角形中心O处场强大小为E,电势为U,选无穷远处电势为零,现将A处的-Q换成+Q,其他条件不变,则中心O处场强大小和电势分别为( )| A. | E,3U | B. | 0,3U | C. | E,U | D. | 0,U |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 某点瞬时速度的方向就在曲线上该点的切线上 | |
| B. | 变速运动一定是曲线运动 | |
| C. | 曲线运动一定是变速运动 | |
| D. | 曲线运动不一定是变速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,电源的电压保持不变,小灯泡L标有“6V 3W”字样,滑动变阻器R1的阻值变化范围为0~20Ω,电阻R2的阻值为12Ω.灯丝的电阻随温度的变化忽略不计.
如图所示,电源的电压保持不变,小灯泡L标有“6V 3W”字样,滑动变阻器R1的阻值变化范围为0~20Ω,电阻R2的阻值为12Ω.灯丝的电阻随温度的变化忽略不计.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 光的粒子性说明每个光子就像一个极小的球体一样 | |
| B. | 光是波,与橡皮绳上的波类似 | |
| C. | 光是一种粒子,它和物质作用是“一份一份”进行的 | |
| D. | 光子在空间各点出现的可能性大小(概率),可以用波动的规律来描述 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 加速前进时,绳拉物体的力大于物体拉绳的力 | |
| B. | 减速前进时,绳拉物体的力小于物体拉绳的力 | |
| C. | 匀速前进时,绳拉物体的力与物体拉绳的力有可能相等,也可能不相等 | |
| D. | 不管物体如何前进,绳拉物体的力与物体拉绳的力大小总相等,因为它们是一对相互作用力 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
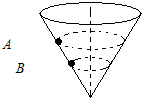 如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )
如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则( )| A. | 线速度vA>vB | B. | 角速度ωA=ωB | C. | 向心力FA=FB | D. | 向心加速度aA<aB |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com