

分析 (1)在AB碰撞过程中,遵守动量守恒定律,由此求出碰后两者的共同速度.再由能量守恒定律求产生的热量.
(2)第一个人与第二个人相距等于第一块物块木板上滑行的过程中木板滑行的距离,由动量守恒定律和动能定理结合求解.
(3)再由动量守恒定律和能量守恒定律结合求长木板上的划痕之和.
解答 解:(1)在AB碰撞过程中,取向右为正方向,由动量守恒定律得:
$\frac{M}{2}$×2v0=($\frac{M}{2}$+$\frac{M}{2}$)v
由能量守恒定律得:
$\frac{1}{2}$×$\frac{M}{2}$×(2v0)2=$\frac{1}{2}$($\frac{M}{2}$+$\frac{M}{2}$)v2+Q
联立解得:Q=$\frac{1}{2}M{v}_{0}^{2}$
(2)第一块物块在木板上滑动的过程,取向右为正方向,由动量守恒定律得:
Mv0=(M+m)v1.
对木板,由动能定理得:
$\frac{1}{2}$Mv12-$\frac{1}{2}$Mv02=-μmgL1.
可得,第一个人与第二个人相距为:L1=$\frac{M(2M+m){v}_{0}^{2}}{2μ(M+m)^{2}g}$
(3)以n个物块和A、B组成的系统为研究对象,对整个过程,由动量守恒定律得:
Mv0=(M+nm)v2.
由能量守恒定律得:
$\frac{1}{2}$Mv02=$\frac{1}{2}$(M+nm)v22+μmgx总.
解得长木板上的划痕之和为:
x总=$\frac{nM{v}_{0}^{2}}{2μ(M+nm)g}$
答:(1)在AB碰撞过程中,产生了$\frac{1}{2}M{v}_{0}^{2}$热量.
(2)第一个人与第二个人相距为$\frac{M(2M+m){v}_{0}^{2}}{2μ(M+m)^{2}g}$.
(3)这n个物块相对木板均静止时,长木板上的划痕之和为$\frac{nM{v}_{0}^{2}}{2μ(M+nm)g}$.
点评 本题要明确非弹性碰撞和相对滑行的过程中,系统遵守的基本规律是:动量守恒定律和能量守恒定律.要知道摩擦产生的热量与相对位移有关.


科目:高中物理 来源: 题型:作图题
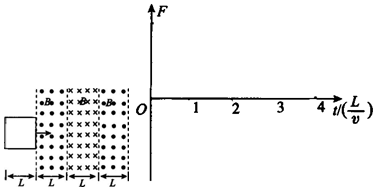
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | a代表行星运动的轨道半径 | B. | k是一个与行星有关的常量 | ||
| C. | T代表行星运动的自转周期 | D. | T代表行星运动的公转周期 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 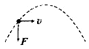 | B. | 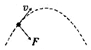 | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为赤道平面内绕地球做匀速圆周运动的卫星,P为B、C两卫星运行轨道的交点.已知A、B、C绕地心运动的周期相等,下列说法正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为赤道平面内绕地球做匀速圆周运动的卫星,P为B、C两卫星运行轨道的交点.已知A、B、C绕地心运动的周期相等,下列说法正确的是( )| A. | 卫星B为地球同步卫星 | |
| B. | 卫星C为地球同步卫星 | |
| C. | 卫星C与物体A的角速度相等 | |
| D. | 卫星B与卫星C在P点时的加速度不相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
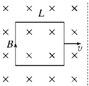 如图所示,边长为L的正方形闭合导线框置于磁感应强度为B的匀强磁场中,线框平面与磁感线的方向垂直.用力将线框分别以速度v1和v2匀速拉出磁场,比较这两个过程,以下判断正确的是( )
如图所示,边长为L的正方形闭合导线框置于磁感应强度为B的匀强磁场中,线框平面与磁感线的方向垂直.用力将线框分别以速度v1和v2匀速拉出磁场,比较这两个过程,以下判断正确的是( )| A. | 若v1>v2,通过线框导线的电荷量q1>q2 | |
| B. | 若v1>v2,拉力F1<F2 | |
| C. | 若v1=2v2,拉力作用的功率P1=2P2 | |
| D. | 若v1=2v2,拉力所做的功W1=2W2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,MN、PQ是水平放置的一对平行金属板,两板接在电压为U的电源两极,上极板MN的中心开有一小孔,在两板之间加一个水平方向的有界匀强磁场,边界为半径为R的圆形,且与MN极板相切与小孔.现将一带电小球从小孔正上方某处由静止释放,小球穿过小孔经磁场偏转后沿直线从下极板右侧Q处离开电场,已知极板长度和间距分别为4$\sqrt{3}$R和3R,磁感应强度为B,重力加速度为g.
如图所示,MN、PQ是水平放置的一对平行金属板,两板接在电压为U的电源两极,上极板MN的中心开有一小孔,在两板之间加一个水平方向的有界匀强磁场,边界为半径为R的圆形,且与MN极板相切与小孔.现将一带电小球从小孔正上方某处由静止释放,小球穿过小孔经磁场偏转后沿直线从下极板右侧Q处离开电场,已知极板长度和间距分别为4$\sqrt{3}$R和3R,磁感应强度为B,重力加速度为g.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )
一质量为m的小球,用长为L的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点移动到Q点,如图所示,关于力F所做的功下列说法正确的是( )| A. | 若水平力F是恒定的力,则力F所做的功为FLsinθ | |
| B. | 若水平力F是恒定的力,则力F所做的功为FL(1-cosθ) | |
| C. | 若是把小球缓慢移动,则力F所做的功为mgL(1-cosθ) | |
| D. | 若是把小球缓慢移动,则力F所做的功为FLsinθ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
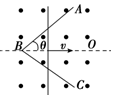 如图所示,横放“V”字形金属框架放在匀强磁场中,磁场与框架平面垂直,金属棒与框架接触良好,框架导体和金属棒电阻率相同,截面积相等,现金属棒从B点开始沿“V”字形角平分线方向做匀速直线运动,那么金属棒脱离框架前,电路中的磁通量Φ、感应电动势E、感应电流I以及金属棒所受到的安培力F随时间变化的图象正确的是 ( )
如图所示,横放“V”字形金属框架放在匀强磁场中,磁场与框架平面垂直,金属棒与框架接触良好,框架导体和金属棒电阻率相同,截面积相等,现金属棒从B点开始沿“V”字形角平分线方向做匀速直线运动,那么金属棒脱离框架前,电路中的磁通量Φ、感应电动势E、感应电流I以及金属棒所受到的安培力F随时间变化的图象正确的是 ( )| A. | 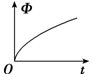 | B. |  | C. | 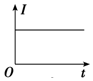 | D. | 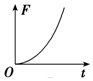 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com