
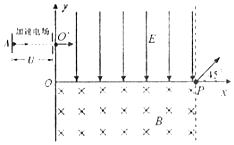
 ��ͼ��ʾ����xOy����ƽ���ڣ���һ��������y�Ḻ�������ǿ�糡�����������д�ֱƽ���������ǿ�ų����糡�ʹų�����߽�Ϊy�ᣬ�ұ߽�Ϊx=3L�����ߣ�x�������ǵķֽ��ߣ���x���Ϸ��ڶ������ڽ���y�����һƽ�а���������������������ӵ�ѹΪU��һ��ֹ������ڲ�A���������ӣ������ٵ糡ֱ���ٺ��Ұ��ϵ�С���������y����O�����ƽ��x�᷽������糡�������ڵ糡�ʹų����˶��������ڴų�����Բ���˶��İ뾶Ϊ$\frac{\sqrt{2}}{2}$L�����ǡ��x���ϵ�P����������������һ���ޣ����ʱ���ٶȷ�����x������ļн�Ϊ45�㣮��֪���ӵ�����Ϊm�������Ϊq�������������ƣ�����
��ͼ��ʾ����xOy����ƽ���ڣ���һ��������y�Ḻ�������ǿ�糡�����������д�ֱƽ���������ǿ�ų����糡�ʹų�����߽�Ϊy�ᣬ�ұ߽�Ϊx=3L�����ߣ�x�������ǵķֽ��ߣ���x���Ϸ��ڶ������ڽ���y�����һƽ�а���������������������ӵ�ѹΪU��һ��ֹ������ڲ�A���������ӣ������ٵ糡ֱ���ٺ��Ұ��ϵ�С���������y����O�����ƽ��x�᷽������糡�������ڵ糡�ʹų����˶��������ڴų�����Բ���˶��İ뾶Ϊ$\frac{\sqrt{2}}{2}$L�����ǡ��x���ϵ�P����������������һ���ޣ����ʱ���ٶȷ�����x������ļн�Ϊ45�㣮��֪���ӵ�����Ϊm�������Ϊq�������������ƣ��������� ��1���������ӵij����ٶȷ��뾶��������ڴų����˶����ҳ������������ں��������µ��ȱ����˶�����������ӽ���ų�ʱ���ٶȷ�������þ���P��ʱ���ٶȣ�
��2�������ӽ���ų�ʱ���ٶȼ�λ�ã�������ƽ���˶�����ȡ����ֱλ�ƣ���O����������ֵ��
��3���������ڴų��˶����ٶȼ��뾶��ôŸ�Ӧǿ�ȣ�������ƽ���˶�����ȡ�õ糡��ǿ��
��� �⣺��1�����ӽ���ų�������������������������Բ���˶���
��ͼ��ʾ���ι�ϵ��֪�������ڴų����˶����ҳ�ΪL��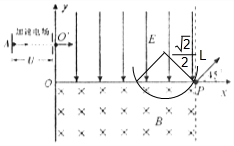 ��
��
���У������ڵ糡���˶�ʱ��ֻ�ܵ糡�������ã���������ˮƽ�����ϵ��ٶȲ��䣬����ֱ�����ϣ����ȱ����˶����ɿ�֪����������ͬλ�����ʴ�С��ͬ��
�������Ӿ����ų������糡���ڽ���ų�ʱ�˶�״̬���һ�ν���ų���ͬ��
�������˶����ҳ�ΪL�ɵ����ӽ���ų��Ĵ���n��ȡ1��2��
��ǰ�������֪�����ӽ���ų�ʱ�ٶȷ�����x���������45�㣬
���Ӿ������ٵ糡�õ��ٶ�v0����$qU=\frac{1}{2}m{{v}_{0}}^{2}$�����ԣ�${v}_{0}=\sqrt{\frac{2qU}{m}}$��
���Ӿ���ƫת�糡ʱ��ˮƽ���ٶȲ��䣬ֻ����ֱ����ķ��ٶȸı䣬���ԣ����ӽ���ų����ٶ�$v=\frac{{v}_{0}}{cos45��}=\sqrt{2}{v}_{0}=2\sqrt{\frac{qU}{m}}$��
�����ڴų���������Բ���˶������ʲ��䣬���ԣ����Ӿ���P��ʱ���ٶȴ�СΪ$2\sqrt{\frac{qU}{m}}$��
��2����O�����������Ϊy���������ڵ糡�е�һ������ƽ���˶����̣�����ų�ʱ�ٶȵ���ֱ����vy=v0tan45��=v0��
����ƽ���˶���x�᷽���λ��x1=2y��
�����ٴλص��糡�е��˶�Ϊ��ƽ�����˶������ݶԳ��Կɵã���2n-1��x1+nL=3L��
���ԣ�$y=\frac{1}{2}{x}_{1}=\frac{1}{2}��\frac{��3-n��L}{2n-1}=\frac{��3-n��L}{2��2n-1��}$��
��n=1ʱ��y=L����n=2ʱ��$y=\frac{1}{6}L$��
��3���������ڴų���ֻ������������������Բ���˶���֪��$Bvq=m\frac{{v}^{2}}{R}$��
���ԣ�$B=\frac{mv}{qR}=\frac{m��2\sqrt{\frac{qU}{m}}}{q��\frac{\sqrt{2}}{2}L}=\frac{2}{L}\sqrt{\frac{2mU}{q}}$��
������ƫת�糡������ƽ���˶������ٶ�$a=\frac{qE}{m}$���˶�ʱ��$t=\frac{2y}{{v}_{0}}$��
������$y=\frac{1}{2}��\frac{qE}{m}����\frac{2y}{{v}_{0}}��^{2}$�����ԣ�$E=\frac{m{{v}_{0}}^{2}}{2qy}=\frac{m��\frac{2qU}{m}}{2qy}=\frac{U}{y}$��
���ԣ���n=1ʱ��y=L��$E=\frac{U}{L}$����n=2ʱ��$y=\frac{1}{6}L$��$E=\frac{6U}{L}$��
�𣺣�l�����Ӿ���P��ʱ���ٶȴ�СΪ$2\sqrt{\frac{qU}{m}}$��
��2��������ֻ����ų�һ��ʱ��O����������ֵΪL�������ӽ���ų�����ʱ��O����������ֵΪ$\frac{1}{6}L$��
��3���ų��ĴŸ�Ӧǿ��BΪ$\frac{2}{L}\sqrt{\frac{2mU}{q}}$��������ֻ����ų�һ��ʱ��ƫת�糡�ij�ǿEΪ$\frac{U}{L}$�������ӽ���ų�����ʱ��ƫת�糡�ij�ǿEΪ$\frac{6U}{L}$��
���� ��������ڴų��е��˶����ⳣ�õ����ι�ϵ���ж����ӵ��˶����籾���У���Ҫ���������ڴų����Ǹ��˶����ҳ����г���Χ���ж����ӵ��˶���ʽ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
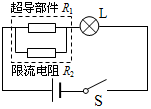 ��ͼ��ʾ��ij��·��ʾ��ͼ�����߿����dz�����������������������һ�ֶ�·���ϵ�������װ�ã����ɳ����������������貢����ɣ���ͨ�����������ĵ����������ٽ����ICʱ�����������ɳ���̬������Ϊ����Ϊ�㣩ת��Ϊ����̬������Ϊ��һ�������裩���Դ������ƹ��ϵ�����������������̬����R1=6�����ٽ����IC=0.6A����������R2=12��������L�ϱ��С�6V��3W����������Դ�綯��E=6V��������Բ��ƣ��������жϲ���ȷ���ǣ�������
��ͼ��ʾ��ij��·��ʾ��ͼ�����߿����dz�����������������������һ�ֶ�·���ϵ�������װ�ã����ɳ����������������貢����ɣ���ͨ�����������ĵ����������ٽ����ICʱ�����������ɳ���̬������Ϊ����Ϊ�㣩ת��Ϊ����̬������Ϊ��һ�������裩���Դ������ƹ��ϵ�����������������̬����R1=6�����ٽ����IC=0.6A����������R2=12��������L�ϱ��С�6V��3W����������Դ�綯��E=6V��������Բ��ƣ��������жϲ���ȷ���ǣ�������| A�� | ��������������ʱ��ͨ����L�ĵ���Ϊ0.5A | |
| B�� | ��������������ʱ��ͨ��R2�ĵ���Ϊ0.5A | |
| C�� | ������L�������϶�·ʱ��ͨ��R1�ĵ���Ϊ1A | |
| D�� | ������L�������϶�·ʱ��ͨ��R2�ĵ���Ϊ0.5A |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
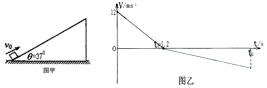 ��ͼ�ף�һ�����壨���Կ����ʵ㣩�Գ��ٶ�v0=12m•s-1��б������㹻����б�����ϳ�ȥ��t1=1.2sʱ������ߵ������б�淵�أ�t2ʱ�̻ص�б��ˣ��˶����ٶ�-ʱ��ͼ����ͼ�ң�б����Ǧ�=37�㣬sin37��=0.6��cos37��=0.8���������ٶ�g=10m•s-2����
��ͼ�ף�һ�����壨���Կ����ʵ㣩�Գ��ٶ�v0=12m•s-1��б������㹻����б�����ϳ�ȥ��t1=1.2sʱ������ߵ������б�淵�أ�t2ʱ�̻ص�б��ˣ��˶����ٶ�-ʱ��ͼ����ͼ�ң�б����Ǧ�=37�㣬sin37��=0.6��cos37��=0.8���������ٶ�g=10m•s-2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
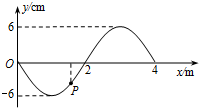 ��ͼ��ʾΪt=0ʱ�̵���x��������ij��г�Შ����ͼ���ʵ�P�ĺ�����
��ͼ��ʾΪt=0ʱ�̵���x��������ij��г�Შ����ͼ���ʵ�P�ĺ������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
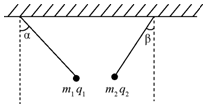 ��ͼ��ʾ�������ֱ���m1��m2�������ֱ�Ϊq1��q2��С���ó��Ȳ��ȵ���˿��������������˿������ֱ����ļнǷֱ��Ǧ��ͦ£������£�����С��ǡ��ͬһˮƽ���ϣ���ô��������
��ͼ��ʾ�������ֱ���m1��m2�������ֱ�Ϊq1��q2��С���ó��Ȳ��ȵ���˿��������������˿������ֱ����ļнǷֱ��Ǧ��ͦ£������£�����С��ǡ��ͬһˮƽ���ϣ���ô��������| A�� | q1һ������q2 | |
| B�� | m1һ��С��m2 | |
| C�� | m1���ܵ���m2 | |
| D�� | m1���ܿ�����һ������m2���ܵĿ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ������ѧ����֪ʶ������⣺
������ѧ����֪ʶ������⣺�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
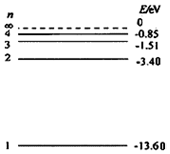 ��֪�����Ƶ��ݳ���Ϊ2.7eV����ԭ�ӵ��ܼ�ͼ��ͼ��ʾ��һȺ��ԭ�Ӵ���������n=4�ܼ�״̬��������
��֪�����Ƶ��ݳ���Ϊ2.7eV����ԭ�ӵ��ܼ�ͼ��ͼ��ʾ��һȺ��ԭ�Ӵ���������n=4�ܼ�״̬��������| A�� | ������2�ܼ���1�ܼ�ԾǨ���Է��������Ϊ10.0ev�Ĺ��� | |
| B�� | ��ԭ�ӿ��ܷ���5��Ƶ�ʵĹ��� | |
| C�� | ��3��Ƶ�ʵķ��������ʹ�Ʒ������ЧӦ | |
| D�� | ��4��Ƶ�ʵķ��������ʹ�Ʒ������ЧӦ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com