
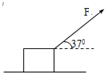
 如图所示,质量m=2kg的木块静止在水平面上,用大小为F=20N,方向与水平方向成37°角的力拉动木块,当木块运动到10m时撤去F.木块与水平面间的动摩擦因数?=0.2.不计空气阻力,g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,质量m=2kg的木块静止在水平面上,用大小为F=20N,方向与水平方向成37°角的力拉动木块,当木块运动到10m时撤去F.木块与水平面间的动摩擦因数?=0.2.不计空气阻力,g=10m/s2,sin37°=0.6,cos37°=0.8.求: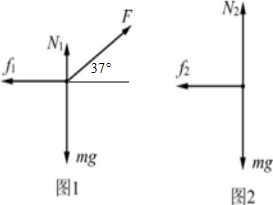
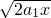 =12m/s
=12m/s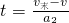 =6.0s
=6.0s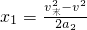 =36m
=36m

 步步高达标卷系列答案
步步高达标卷系列答案科目:高中物理 来源: 题型:
 (2013?荆州模拟)如图所示,质量m=2.2kg的金属块放在水平地板上,在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下,以速度v=5.0m/s向右做匀速直线运动.(cos37°=0.8,sin37°=0.6,取g=10m/s2)求:
(2013?荆州模拟)如图所示,质量m=2.2kg的金属块放在水平地板上,在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下,以速度v=5.0m/s向右做匀速直线运动.(cos37°=0.8,sin37°=0.6,取g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量m=2.0kg的木块静止在水平面上,用大小F=20N、方向与水平方向成θ=37°角的力拉动木块,当木块运动到x=10m时撤去力F.不计空气阻力.已知木块与水平面间的动摩擦因数?=0.2,sin37°=0.6,cos37°=0.8.g取10m/s2.求:
如图所示,质量m=2.0kg的木块静止在水平面上,用大小F=20N、方向与水平方向成θ=37°角的力拉动木块,当木块运动到x=10m时撤去力F.不计空气阻力.已知木块与水平面间的动摩擦因数?=0.2,sin37°=0.6,cos37°=0.8.g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量m=2.0×104kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m.由于轮胎太旧,如果受到超过3×105N的压力时就会出现爆胎,则:
如图所示,质量m=2.0×104kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20m.由于轮胎太旧,如果受到超过3×105N的压力时就会出现爆胎,则:查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,质量m=2.0kg的金属块放在水平地板上,在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下,以速度v=5.0m/s向右做匀速直线运动.(cos37°=0.8,sin37°=0.6,取g=10m/s2)求:
如图所示,质量m=2.0kg的金属块放在水平地板上,在与水平方向成θ=37°角斜向上、大小为F=10N的拉力作用下,以速度v=5.0m/s向右做匀速直线运动.(cos37°=0.8,sin37°=0.6,取g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:
 (2013?海淀区一模)如图所示,质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的电场强度为E1的匀强电场中.取g=10m/s2.
(2013?海淀区一模)如图所示,质量m=2.0×10-4kg、电荷量q=1.0×10-6C的带正电微粒静止在空间范围足够大的电场强度为E1的匀强电场中.取g=10m/s2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com