
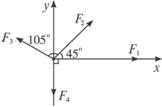
图5-2-20
解析:建立平面直角坐标系,运用正交分解法将所有的力在坐标轴上投影,可求多个共点力的合力.在图中先建立如图所示的坐标系(如图),对每一个力进行正交分解并求每一个力在x轴和y轴上的分力:

F1x=F1,F1y=0
F2x=F2cos45°,F2y=F2sin45°
F3x=F3cos150°,F3y=F3sin150°
F4x=0,F4y=-F4
再分别算出x轴和y轴方向的合力
Fx=F1x+F2x+F3x+F4x=F1+F2cos45°+F3cos150°
=(60+40×![]() -30
-30![]() )N≈62.3 N
)N≈62.3 N
Fy=F1y+F2y+F3y+F4y=F2sin45°+F3sin150°-F4=(40×![]() -30×
-30×![]() -25) N≈18.3 N
-25) N≈18.3 N
于是总合力F=![]() =65 N
=65 N
tanθ=Fy/Fx=18.3/62.3≈0.294
故θ≈16.4
对于在同一平面内的两个以上的共点力的合成,利用多边形合成的作图法把合力作出来是方便的,但容易引起较大的误差.如果要按照多边形合成的计算法把合力计算出来,又显得很烦琐,如果用正交分解法先分解后合成,计算过程就简便得多.正交分解法实际上是为了更方便地求合力.


科目:高中物理 来源: 题型:
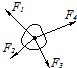 如图所示,作用在物体上的同一平面内的四个共点力合力为零,若其中F2、F3、F4大小和方向保持不变,F1逆时针方向转过90°,而大小保持不变,则此物体所受的合力大小为( )
如图所示,作用在物体上的同一平面内的四个共点力合力为零,若其中F2、F3、F4大小和方向保持不变,F1逆时针方向转过90°,而大小保持不变,则此物体所受的合力大小为( )查看答案和解析>>
科目:高中物理 来源:设计必修一物理 鲁科版 题型:038
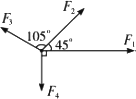
在同一平面上的四个共点力F1、F2、F3、F4的量值依次为60 N、40 N、30 N、25 N,方向如图所示.试求其合力.
查看答案和解析>>
科目:高中物理 来源:2012-2013学年福建晋江季延中学高一上学期期中物理试卷(带解析) 题型:单选题
如图所示,作用在物体上的同一平面内的四个共点力合力为零,若其中F2、F3、F4大小和方向保持不变,F1逆时针方向转过900,而大小保持不变,则此物体所受的合力大小为( )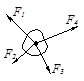
A.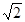 F1 F1 | B.2F2 | C.F1 | D.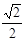 F1 F1 |
查看答案和解析>>
科目:高中物理 来源:2015届福建晋江季延中学高一上学期期中物理试卷(解析版) 题型:选择题
如图所示,作用在物体上的同一平面内的四个共点力合力为零,若其中F2、F3、F4大小和方向保持不变,F1逆时针方向转过900,而大小保持不变,则此物体所受的合力大小为( )

A. F1 B.2F2 C.F1 D.
F1 B.2F2 C.F1 D.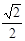 F1
F1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com