
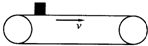
 如图:一水平传送带以2m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由左端运动到右端所经历的时间为11s,则:
如图:一水平传送带以2m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由左端运动到右端所经历的时间为11s,则: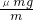 =μg
=μg =
=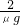
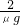
 at12+vt2=20m
at12+vt2=20m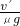 =4m/s2
=4m/s2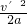 =8m
=8m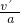 =4s
=4s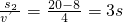


科目:高中物理 来源: 题型:
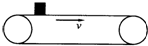 如图:一水平传送带以4m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由一端运动到另一端所经历的时间为6s,则物体与传送带之间的摩擦系数是多少?如果需要在最短的时间内把静止的物体从左端传送到右端,则传送带的速度至少应该是多少?
如图:一水平传送带以4m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由一端运动到另一端所经历的时间为6s,则物体与传送带之间的摩擦系数是多少?如果需要在最短的时间内把静止的物体从左端传送到右端,则传送带的速度至少应该是多少?查看答案和解析>>
科目:高中物理 来源: 题型:
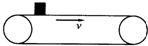
 如图:一水平传送带以2m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由左端运动到右端所经历的时间为11s,则:
如图:一水平传送带以2m/s的速度做匀速直线运动,传送带上两端的距离为20m,将一物体轻轻地放在传送带的一端,物体由左端运动到右端所经历的时间为11s,则:查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
查看答案和解析>>
科目:高中物理 来源:2010-2011学年江苏省苏州市张家港市暨阳中学高一(上)月考物理试卷(12月份)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com