练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
    如图6-3所示,A是地球的同步卫星,另一卫星B的圆形轨道位于赤道平面内,离地面高度为h.已知地球半径为R,地球自转角速度为ω0,地球表面的重力加速度为g,O为地球中心.

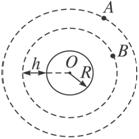
    图6-3

    (1)求卫星B的运行周期.

    (2)如卫星B绕行方向与地球自转方向相同,某时刻A、B两卫星相距最近(O、B、A在同一直线上),则至少经过多长时间,它们再一次相距最近?

    解析:(1)由万有引力定律和向心力公式得

                        ①

        =mg                              ②

        联立①②得TB=2π.              ③

    (2)由题意得(ωB-ω0)t=2π                        ④

        由③得ωB=                    ⑤

        代入④得t=.

    答案:(1)2π  (2)

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：

    如图6-3所示，M、N是两个共轴圆筒的横截面，外筒半径为R，内筒半径比R小很多，可以忽略不计，筒的两端是封闭的，两筒之间成真空.两筒以相同的角速度ω绕其中心轴线（图中垂直于纸面）做匀速运动，设从M筒内部可以通过窄缝s（与M筒的轴线平行）不断地向外射出两种不同速率v1和v2的微粒，从s处射出时的初速度的方向都是沿筒的半径方向，微粒到达N筒后就附着在N筒上.如果R、v1和v2都不变，而ω取某一合适的值，则（    ）

    图6-3

    A.有可能使微粒落在N筒上的位置都在a处一条与s缝平行的窄条上

    B.有可能使微粒落在N筒上的位置都在某一处，如b处一条与s缝平行的窄条上

    C.有可能使微粒落在N筒上的位置分别在某两处，如b处和c处与s缝平行的窄条上

    D.只要时间足够长，N筒上将到处都落有微粒

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    如图6-2所示，一质量为m的物体系于长度分别为l1、l2的两根细线上，l1的一端悬挂在天花板上，与竖直方向夹角为θ,l2水平拉直，物体处于平衡状态.现将l2线剪断，求剪断瞬时物体的加速度.

    图6-2

    （1）下面是某同学对该题的一种解法：

    解：设l1线上拉力为T1，l2线上拉力为T2，重力为mg，物体在三力作用下保持平衡.

    T1cosθ=mg,T1sinθ=T2

    T2=mgtanθ

        剪断线的瞬间，T2突然消失，物体即在T2反方向获得加速度.

        因为mgtanθ=ma，所以加速度a=gtanθ,方向与T2反方向，你认为这个结果正确吗？请对该解法作出评价并说明理由.

    （2）若将图6-2中的细线l1改为长度相同、质量不计的轻弹簧，如图6-3所示，其他条件不变，求解的步骤和结果与（1）完全相同，即a=gtanθ，你认为这个结果正确吗？请说明理由.

    图6-3

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    一弹簧振子做简谐运动，振动图象如图6—3所示。振子依次振动到图中a、b、c、d、e、f、g、h各点对应的时刻时，（1）在哪些时刻，弹簧振子具有：沿x轴正方向的最大加速度；沿x轴正方向的最大速度。（2）弹簧振子由c 点对应x轴的位置运动到e点对应x轴的位置，和由e点对应x轴的位置运动到g点对应x轴的位置所用时间均为0.4s。弹簧振子振动的周期是多少？（3）弹簧振子由e点对应时刻振动到g点对应时刻，它在x轴上通过的路程是6cm，求弹簧振子振动的振幅。

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    一弹簧振子做简谐运动，振动图象如图6—3所示。振子依次振动到图中a、b、c、d、e、f、g、h各点对应的时刻时，（1）在哪些时刻，弹簧振子具有：沿x轴正方向的最大加速度；沿x轴正方向的最大速度。（2）弹簧振子由c 点对应x轴的位置运动到e点对应x轴的位置，和由e点对应x轴的位置运动到g点对应x轴的位置所用时间均为0.4s。弹簧振子振动的周期是多少？（3）弹簧振子由e点对应时刻振动到g点对应时刻，它在x轴上通过的路程是6cm，求弹簧振子振动的振幅。

    查看答案和解析>>

    同步练习册答案