
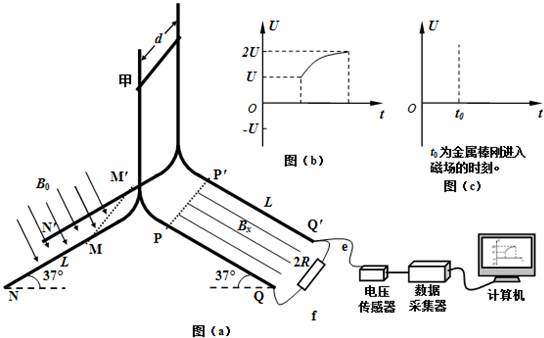
分析 (1)有左手定则判定电流方向;
(2)根据图象求得电压对应的速度,利用动能定理求得下降时的高度;
(3)由动能定理求得产生的热量;
(4)通过牛顿第二定律分别求得,两棒的加速度表达式,根据两者之间的关系确定力的关系;
解答 解:(1)对甲棒,利用左手定则确定感应电流的方向由M′到M,此时MM′相当于电源,f为正极引线.
(2)由图象知:棒进入磁场时定值电阻2R的电压为U,通过的电流,I=$\frac{U}{2R}$,
有闭合电路欧姆定律可知,此时的电动势,E=IR总=$\frac{U}{2R}×3R=\frac{3}{2}U$,
有电磁感应定律得:E=B0dv1,解得:v1=$\frac{3U}{2{B}_{0}d}$,
由动能定理得:mgh=$\frac{1}{2}$mv12,
解得:h=$\frac{9{U}^{2}}{8g{d}^{2}{B}_{0}^{2}}$
(3)当甲棒离开磁场时的速度为v2,有(2)中电磁感应知识结合电路特点得,$2U=\frac{2R}{3R}{B_0}d{v_2}=\frac{2}{3}{B_0}d{v_2}$
解得:${v}_{2}=\frac{3U}{{B}_{0}d}$
对甲棒,由动能定理,有$mgLsin{37°}-μmgLcos{37°}-{Q_总}=\frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2$,
式中Q总为克服安培力所做的功,转化成了甲、乙棒上产生的热量;${Q_总}=\frac{1}{2}mgL-\frac{{27m{U^2}}}{{8B_0^2{d^2}}}$
有串并联电路特点:定值电阻上产生的热量,Q=$\frac{2}{3}{Q}_{总}$=$\frac{1}{3}mgL-\frac{9m{U}^{2}}{4{B}_{0}^{2}{d}^{2}}$,
(4)两棒由静止释放的高度越高,甲棒进入磁场时的安培力越大,加速度越小,而乙棒只有摩擦力越大加速度才越小,故乙棒所受安培力应垂直斜面向下
由右手定则得:Bx沿斜面向下;
从不同高度下落两棒总是同时到达桌面,说明两棒运动的加速度时刻相同.
对甲棒,根据牛顿第二定律,有
$mgsinθ-μmgcosθ-\frac{{B}_{0}^{2}{d}^{2}v}{2R}=ma$
对乙棒,根据牛顿第二定律,有
$2mgsinθ-μ(2mgcosθ+{B}_{X}×\frac{1}{2}×\frac{{B}_{0}dv}{2r}d)$=2ma
所以:$\frac{μ{B}_{X}{B}_{0}{d}^{2}v}{8R}=\frac{{B}_{0}^{2}{d}^{2}v}{2R}$
解得:BX=$\frac{4}{μ}{B}_{0}$=32B0
操作Ⅱ中计算机屏幕上可能出现的U-t关系图象有三种可能,如图(c)所示.
答;(1)f为正极引线;
(2)甲释放时距MM′的高度h$\frac{9{U}^{2}}{8g{d}^{2}{B}_{0}^{2}}$
(3)试求操作Ⅰ中定值电阻上产生的热量Q=$\frac{1}{3}mgL-\frac{9m{U}^{2}}{4{B}_{0}^{2}{d}^{2}}$;
(4)匀强磁场Bx的方向沿斜面向下,大小为32B0,U-t关系图象如图: .
.
点评 本题综合考查了切割产生的感应电动势公式、闭合电路欧姆定律、共点力平衡、能量守恒等知识,综合性较强,需加强训练.


科目:高中物理 来源: 题型:解答题
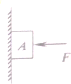 如图 6--4所示,在F作用下,质量为10kg的物体A静止在竖直墙上,这时F=50N,如果F增大为100N,A还静止在墙上,在这两种情况下,A所受到的摩擦力如何变化?(g取10m/s2)
如图 6--4所示,在F作用下,质量为10kg的物体A静止在竖直墙上,这时F=50N,如果F增大为100N,A还静止在墙上,在这两种情况下,A所受到的摩擦力如何变化?(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
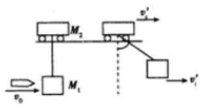 质量为M=18kg的小车放在光滑轨道上,小车下用一根长L=1m的轻绳系一质量M1=1.99kg的木块,一质量m=0.01kg的子弹,以速度v0水平射入木块并留在其中,之后测得木块能摆起的最大摆角θ=60°,求子弹的速度v0(g取10m/s2)
质量为M=18kg的小车放在光滑轨道上,小车下用一根长L=1m的轻绳系一质量M1=1.99kg的木块,一质量m=0.01kg的子弹,以速度v0水平射入木块并留在其中,之后测得木块能摆起的最大摆角θ=60°,求子弹的速度v0(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 0V | B. | 约0.8V | C. | 12V | D. | 120V |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
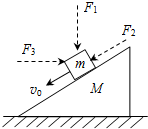 一斜劈静止于粗糙的水平地面上,在其斜面上放一滑块m,若给m一向下的初速度v0,则m正好保持匀速下滑.如图所示,现在m下滑的过程中再加一个作用力,则以下说法正确的是( )
一斜劈静止于粗糙的水平地面上,在其斜面上放一滑块m,若给m一向下的初速度v0,则m正好保持匀速下滑.如图所示,现在m下滑的过程中再加一个作用力,则以下说法正确的是( )| A. | 在m上加一竖直向下的力F1,则m将保持匀速运动,M对地无静摩擦力的作用 | |
| B. | 在m上加一个沿斜面向下的力F2,则m将做加速运动,M对地有水平向左的静摩擦力的作用 | |
| C. | 在m上加一个水平向右的力F3,则m将做减速运动,在m停止前M对地有向右的静摩擦力的作用 | |
| D. | 无论在m上加什么方向的力,在m沿斜面向下运动的过程中,M对地都无静摩擦力的作用 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 关于做“测电源电动势和内阻”的实验.某同学通过改变滑动变阻器的电阻,测得了6组U、I的数据,根据第1、2、3、4、5和6组的数据,他在U-I图上标出了这些数据点,并且按照这些数据点的分布绘制了相应的U-I图线[如图所示],由这一图线,可求得电源的电动势E为1.45V,内电阻r为0.5Ω.如果他不利用这一图线,而是利用任意两组U、I数据,那么当他选择哪二组数据求出的E、r值时误差最大?答:2、3(写数据组编号如1和2;3和4;5和6).
关于做“测电源电动势和内阻”的实验.某同学通过改变滑动变阻器的电阻,测得了6组U、I的数据,根据第1、2、3、4、5和6组的数据,他在U-I图上标出了这些数据点,并且按照这些数据点的分布绘制了相应的U-I图线[如图所示],由这一图线,可求得电源的电动势E为1.45V,内电阻r为0.5Ω.如果他不利用这一图线,而是利用任意两组U、I数据,那么当他选择哪二组数据求出的E、r值时误差最大?答:2、3(写数据组编号如1和2;3和4;5和6).查看答案和解析>>
科目:高中物理 来源: 题型:选择题
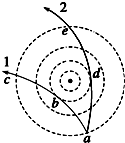 如图所示,虚线为某点电荷电场的等势面,现有两个重力可忽略不计的带电粒子,其比荷相同,二者以相同的速率从同一等势面的a点进入电场后沿不同的轨迹1和2运动,图中a、b、c、d、e是粒子轨迹与各等势面的交点,则可以判断( )
如图所示,虚线为某点电荷电场的等势面,现有两个重力可忽略不计的带电粒子,其比荷相同,二者以相同的速率从同一等势面的a点进入电场后沿不同的轨迹1和2运动,图中a、b、c、d、e是粒子轨迹与各等势面的交点,则可以判断( )| A. | 两个粒子的电性相同 | |
| B. | 经过b、d两点时,两粒子的速率相等 | |
| C. | 经过b、d两点时,两粒子的加速度大小相等 | |
| D. | 经过c、e两点时,两粒子的电势能相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
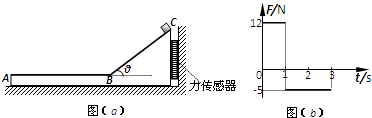 如图(a)所示,“
如图(a)所示,“ ”型木块放在光滑水平地面上,木块水平表面AB粗糙,BC表面光滑且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:
”型木块放在光滑水平地面上,木块水平表面AB粗糙,BC表面光滑且与水平面夹角为θ=37°.木块右侧与竖直墙壁之间连接着一个力传感器,当力传感器受压时,其示数为正值;当力传感器被拉时,其示数为负值.一个可视为质点的滑块从C点由静止开始下滑,运动过程中,传感器记录到的力和时间的关系如图(b)所示.已知sin37°=0.6,cos37°=0.8,g取10m/s2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com