
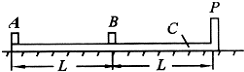
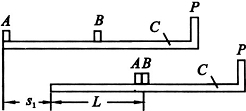
 (2009?武汉模拟)如图所示,在水平桌面上放有长木板C,C上右端是固定挡板P,在C上左端和中点处各放有小物块A和B,A、B的尺寸以及P的厚度皆可忽略不计,A、B之间和B、P之间的距离皆为L.设木板C与桌面之间无摩擦,A、C之间和B、C之间的静摩擦因数及滑动摩擦因数均为μ;A、B、C(连同挡板P)的质量相同.开始时,B和C静止,A以某一初速度向右运动.试问下列情况是否能发生?要求定量求出能发生这些情况时物块A的初速度V0应满足的条件,或定量说明不能发生的理由.
(2009?武汉模拟)如图所示,在水平桌面上放有长木板C,C上右端是固定挡板P,在C上左端和中点处各放有小物块A和B,A、B的尺寸以及P的厚度皆可忽略不计,A、B之间和B、P之间的距离皆为L.设木板C与桌面之间无摩擦,A、C之间和B、C之间的静摩擦因数及滑动摩擦因数均为μ;A、B、C(连同挡板P)的质量相同.开始时,B和C静止,A以某一初速度向右运动.试问下列情况是否能发生?要求定量求出能发生这些情况时物块A的初速度V0应满足的条件,或定量说明不能发生的理由.| v | 0 |
| a | A |
| a | B |
| a | C |
| a | A |
| a | C |
| a | B |
| a | B |
| a | C |
| a | B |
| a | C |
| 1 |
| 2 |
| v | 1 |
| v | 0 |
| v | 1 |
| S | 1 |
| S | 1 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
| S | 1 |
| 1 |
| 2 |
| v | 2 1 |
| gS | 1 |
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| v | 2 0 |
| v | 0 |
| 3μmgL |
| v | 0 |
| 3μmgL |
| v | 0 |
| 3μmgL |
| v | 0 |
| 3μmgL |
| v | 0 |
| 3μmgL |
| v | 0 |
| v | A |
| v | B |
| v | C |
| v | A |
| v | B |
| v | B |
| v | C |
| v | ′ A |
| v | ′ B |
| v | ′ C |
| v | ′ A |
| v | B |
| v | ′ B |
| v | A |
| v | ′ C |
| v | C |
| v | ′ B |
| v | 2 |
| v | 0 |
| v | 2 |
| v | 0 |
| 1 |
| 2 |
| v | 2 2 |
| 1 |
| 2 |
| v | 2 0 |
| v | 0 |
| 6μmgL |
| v | 0 |
| 6μmgL |
| v | 0 |
| 6μmgL |
| v | 0 |
| 6μmgL |
| v | 0 |
| 6μmgL |
| v | 0 |
| v | ″ A |
| v | ″ B |
| v | ″ C |
| v | ″ B |
| v | ″ A |
| v | ″ C |
| v | ″′ A |
| v | ″′ B |
| v | ′″ C |
| v | ″′ B |
| v | ″ C |
| v | ″′ C |
| v | ″ B |
|
| v | ″ A |
| v | ″′ C |
| v | ″ A |
| v | ″′ B |
| a | C |
| a | A |
| a | B |
| 0 |
| v | 3 |
| v | 3 |
| v | 0 |
| v | 0 |
| 1 |
| 2 |
| v | 2 3 |
| 1 |
| 2 |
| v | 2 0 |
| v | 0 |
| 12μgL |
| v | 0 |
| 12μgL |
| v | 0 |
| 12μgL |
| v | 0 |
| 12μgL |
| v | 0 |
| 12μgL |
| v | 0 |
| v | ″′ A |
| v | ″′ B |
| v | ″ C |
| v | ″′ A |
| v | ″′ B |
| v | ″′ C |
| v | 0 |
| mv | ″″ A |
| mv | ″″ C |
| 1 |
| 2 |
| (2m)v | ″″2 B |
| 1 |
| 2 |
| v | ″″2 C |
| 1 |
| 2 |
| v | 2 0 |
| v | 4 |
| v | ″″ B |
| v | ″″ C |
| v | 4 |
| 1 |
| 2 |
| (2m)v | 2 4 |
| 1 |
| 2 |
| mv | ″″2 B |
| 1 |
| 2 |
| mv | ″″2 C |
| v | 0 |
| μmgL |
| v | 0 |
| μmgL |
| v | 0 |
| μmgL |
| v | 0 |
| μmgL |


科目:高中物理 来源: 题型:
 (2009?武汉模拟)一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )
(2009?武汉模拟)一列简谐波某时刻的波形如图中实线所示.经过0.5s后的波形如图中的虚线所示.已知波的周期为T,且0.25s<T<0.5s,则( )查看答案和解析>>
科目:高中物理 来源: 题型:
 (2009?武汉模拟)如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两电极之间的电压U应是多少?(不计重力,整个装置在真空中)
(2009?武汉模拟)如图,两个共轴的圆筒形金属电极,外电极接地,其上均匀分布着平行于轴线的四条狭缝a、b、c和d,外筒的外半径为r.在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场,磁感应强度的大小为B.在两极间加上电压,使两圆筒之间的区域内有沿半径向外的电场.一质量为m、带电量为+q的粒子,从紧靠内筒且正对狭缝a的S点出发,初速为零.如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两电极之间的电压U应是多少?(不计重力,整个装置在真空中)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com