
| 1 |
| 2 |
| v | 2 0 |
| 2gH |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
| 3mA-mB |
| mA+mB |
| ||
| 2g |
| 3mA-mB |
| mA+mB |
| 3mA-mB |
| mA+mB |


科目:高中物理 来源: 题型:
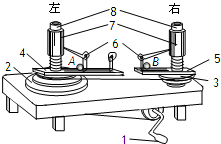 (2011?海淀区模拟)向心力演示器如图所示.转动手柄1,可使变速塔轮2和3以及长槽4和短槽5随之匀速转动,槽内的小球就做匀速圆周运动.小球做圆周运动的向心力由横臂6的挡板对小球的压力提供,球对挡板的反作用力通过横臂的杠杆使弹簧测力套筒7下降,从而露出标尺8,标尺8上露出的红白相间等分格子的多少可以显示出两个球所受向心力的大小.皮带分别套在塔轮2和3上的不同圆盘上,可改变两个塔轮的转速比,以探究物体做圆周运动的向心力大小跟哪些因素有关、具体关系怎样.现将小球A和B分别放在两边的槽内,小球A和B的质量分别为mA和mB,做圆周运动的半径分别为rA和rB.皮带套在两塔轮半径相同的两个轮子上,实验现象显示标尺8上左边露出的等分格子多于右边,则下列说法正确的( )
(2011?海淀区模拟)向心力演示器如图所示.转动手柄1,可使变速塔轮2和3以及长槽4和短槽5随之匀速转动,槽内的小球就做匀速圆周运动.小球做圆周运动的向心力由横臂6的挡板对小球的压力提供,球对挡板的反作用力通过横臂的杠杆使弹簧测力套筒7下降,从而露出标尺8,标尺8上露出的红白相间等分格子的多少可以显示出两个球所受向心力的大小.皮带分别套在塔轮2和3上的不同圆盘上,可改变两个塔轮的转速比,以探究物体做圆周运动的向心力大小跟哪些因素有关、具体关系怎样.现将小球A和B分别放在两边的槽内,小球A和B的质量分别为mA和mB,做圆周运动的半径分别为rA和rB.皮带套在两塔轮半径相同的两个轮子上,实验现象显示标尺8上左边露出的等分格子多于右边,则下列说法正确的( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,已知小球a和b的质量分别为
如图所示,两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,已知小球a和b的质量分别为| 3 |
| 2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,已知小球a和b的质量分别为
如图所示,两个可视为质点的小球a和b,用质量可忽略的刚性细杆相连,放置在一个光滑的半球面内,已知小球a和b的质量分别为| 3 |
| 2 |
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com