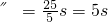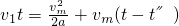在平直公路上一辆值勤警车停在路边,突然警察发现一违规卡车以72km/h 的速度从旁边匀速驶过,4s后警察启动警车追赶卡车,警车加速阶段可看作匀加速直线运动,加速度a=5m/s2,此路段警车的最大时速为90km/h.试求:
(1)两车相距最远时两车间的距离;
(2)从警车发现卡车到追上卡车所需要的时间?
解:(1)72km/h=20m/s
当速度相等时,两车相距最远,
知t=
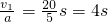
.
此时卡车的位移x
1=v
1t=80m.
警车的位移

,
则相距的最远距离△x=x
1-x
2=40m.
(2)根据
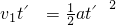
得,t′=8s.
此时警车的速度v′=at′=40m/s>25m/s=90km/h.
知警车先匀加速追赶,达到最大速度后匀速追赶.
设经过t后追上,警车达到最大速度所需的时间为t
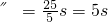
则有
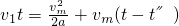
解得t=12.5s.
答:(1)两车相距最远时两车间的距离为40m.
(2)从警车发现卡车到追上卡车所需要的时间为12.5s.
分析:(1)当两车速度相等时,两车相距最远,通过匀变速直线运动的速度时间公式和位移公式求出相距的最远距离.
(2)抓住位移相等,根据运动学公式求出追及的时间.
点评:解决本题的关键知道速度相等时,两车相距最远,掌握匀变速直线运动的运动学公式,并能灵活求解.

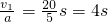 .
. ,
,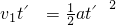 得,t′=8s.
得,t′=8s.