

分析 (1)根据动能定理,选取电子打到荧光屏上作为过程,即可求解;
(2)根据电子束最大偏转,得出PQ的长度,由三角函数,可求出θ,再根据几何关系,与牛顿第二定律及洛伦兹力公式,即可求解;
(3)根据电子在磁场中转过的圆心角与电子做圆周运动的周期公式求出电子的运动时间.
解答 解:(1)电子打到荧光屏上时速度的大小等于它飞出加速电场的速度大小,由动能定理得:eU=$\frac{1}{2}$mv2-0,
解得:v=$\sqrt{\frac{2eU}{m}}$;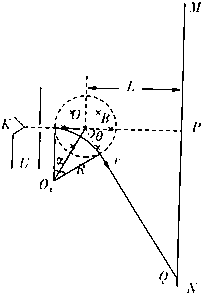
(2)当磁感应强度为峰值B0时,电子束有最大偏转,在荧光屏上打在Q点.则有:
PQ=$\sqrt{3}$L,电子运动轨迹如图所示,
设此时的偏转角为θ,由几何关系可知,
tanθ=$\frac{\sqrt{3}L}{L}$,
解得:θ=60°,
根据几何关系,电子束在磁场中运动路径所对圆心角α=θ,
而tan$\frac{α}{2}$=$\frac{r}{R}$,
由牛顿第二定律得:evB0=m$\frac{{v}^{2}}{R}$,
解得:B0=$\frac{\sqrt{6meU}}{3er}$;
(3)电子在磁场中做圆周运动的周期:T=$\frac{2πm}{e{B}_{0}}$=$\frac{6πmr}{\sqrt{6meU}}$,
电子在磁场中转过的圆心角:α=60°,
电子在磁场中的运动时间:t=$\frac{α}{360°}$T=$\frac{1}{6}$T=$\frac{πmr}{\sqrt{6meU}}$;
答:(1)电子打到荧光屏上时速度的大小为$\sqrt{\frac{2eU}{m}}$;
(2)磁场磁感应强度的最大值为$\frac{\sqrt{6meU}}{3er}$;
(3)磁感应强度为B0时,电子通过磁场区的时间为$\frac{πmr}{\sqrt{6meU}}$.
点评 考查动能定理的应用,掌握牛顿第二定律与洛伦兹力公式的综合,理解几何关系正确的运用,注意正确画出运动轨迹图,建立已知长度与半径的关系,是解题的关键.


科目:高中物理 来源: 题型:选择题

| A. | S1接通,S2、S3断开,日光灯就能正常发光 | |
| B. | S1、S2接通,S3断开,日光灯就能正常发光 | |
| C. | S3断开,接通S1、S2后,再断开S2,日光灯就能正常发光 | |
| D. | S1、S2、S3接通,日光灯就能正常发光 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 一个质量为0.3kg的物体沿水平面做直线运动,如图所示,图线a表示物体受水平拉力时的v-t图象,图线b表示撤去水平拉力后物体继续运动的v-t图象,下列说法正确的是( )
一个质量为0.3kg的物体沿水平面做直线运动,如图所示,图线a表示物体受水平拉力时的v-t图象,图线b表示撤去水平拉力后物体继续运动的v-t图象,下列说法正确的是( )| A. | 水平拉力的大小为0.1N,方向与摩擦力方向相同 | |
| B. | 水平拉力作用下物体滑行12m | |
| C. | 撤去拉力后物体还能滑行7.5m | |
| D. | 物体与水平面间的动摩擦因数为0.1 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | “玉兔号”月球车在地球表面与月球表面质量之比为$\frac{{G}_{1}}{{G}_{2}}$ | |
| B. | 地球表面处的重力加速度与月球表面处的重力加速度之比为$\frac{{G}_{2}}{{G}_{1}}$ | |
| C. | 地球的质量与月球的质量之比为$\frac{{G}_{1}{{R}_{2}}^{2}}{{G}_{2}{{R}_{1}}^{2}}$ | |
| D. | 地球的第一宇宙速度与月球的第一宇宙速度之比为$\sqrt{\frac{{G}_{1}{R}_{1}}{{G}_{2}{R}_{2}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示.物块的质量为m,它与水平桌面间的动摩擦因数μ,期初,用手拉物块,弹簧的伸长量为x.放手后,物块向左运动至弹簧压缩量为y时停下,当弹簧的长度恢复原长时,物块的速度为v,则( )
如图所示.物块的质量为m,它与水平桌面间的动摩擦因数μ,期初,用手拉物块,弹簧的伸长量为x.放手后,物块向左运动至弹簧压缩量为y时停下,当弹簧的长度恢复原长时,物块的速度为v,则( )| A. | x>y | |
| B. | 物块运动过程中的最大速度为v | |
| C. | 全过程弹簧弹性势能的减小量为μmg(x+y) | |
| D. | 从物块开始运动到弹簧恢复原长的过程中弹力做功$\frac{1}{2}$mv2-μmgx |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
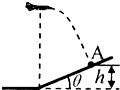 如图所示,轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知A点高度为h,山坡倾角为θ,由此可算出( )
如图所示,轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知A点高度为h,山坡倾角为θ,由此可算出( )| A. | 轰炸机的飞行高度 | B. | 轰炸机的飞行速度 | ||
| C. | 炸弹的飞行时间 | D. | 炸弹投出时的速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com