

分析 (1)A在光滑曲面上下滑过程,遵守机械能守恒,由机械能守恒定律求出A与B第一次碰撞前的速度.A、B碰撞过程,遵守动量守恒和机械能守恒,据两大守恒定律列式,求出碰后A、B的速度.
(2)A与B第一次碰撞后A做匀加速直线运动,B做匀减速运动,根据牛顿第二定律和运动学公式求解A与B第二次碰撞前A的速度,再根据碰撞的规律求解B获得的速度.
(3)假设A与B完成第二次碰撞后的同时撤去电场,A将静止,此时B距C的左端距离为 l=d-xB,由速度位移公式求出B刚滑上C的速度.由动量守恒定律求出B与C在第一次与挡板P碰前的共同速度,C与挡板碰撞后向左减速运动,运用数学归纳法分析C每次向左运动的最大距离,再求解总路程.
解答 解:(1)设mA=mB=m,
A在光滑曲面上下滑过程,由机械能守恒得:mgh=$\frac{1}{2}m{v}^{2}$,
可得A与B第一次碰撞前的速度为:v=$\sqrt{2gh}$=$\sqrt{2×10×3.2}$m/s=8m/s,
A、B碰撞过程,取向右为正方向,由动量守恒和机械能守恒得:
mv=mvA+mvB
$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}m{v}_{A}^{2}$+$\frac{1}{2}m{v}_{B}^{2}$
可得A与B第一次碰撞后A的速度为:vA=0,vB=8m/s;
(2)A与B第一次碰撞后A做匀加速直线运动,加速度大小为:a1=$\frac{qE-μmg}{m}$=$\frac{5×1{0}^{-2}×1{0}^{2}-0.4×1×10}{1}$=1m/s2;
B做匀减速直线运动,加速度大小为:a2=$\frac{μmg}{m}$=μg=4m/s2;
B的速度减到零所需的时间为:tB=$\frac{{v}_{B}}{{a}_{2}}$=$\frac{8}{4}$s=2s,
位移为为:xB=$\frac{{v}_{B}t}{2}$=$\frac{8×2}{2}$m=8m
而A做匀加速直线运动2s发生的位移为为:
xA=$\frac{1}{2}{a}_{1}{t}_{B}^{2}$=$\frac{1}{2}×1×{2}^{2}$m=2m<xB=8m
所以当B的速度减到零以后才发生第二次碰撞,第二次碰撞前A的速度为为:vA′=$\sqrt{2{a}_{1}{x}_{B}}$=$\sqrt{2×1×8}$m/s=4m/s
由动量守恒定律和碰撞过程能量守恒可得:A与B第二次碰撞后B获得的速度为:vB′=4m/s;
(3)假设A与B完成第二次碰撞后的同时撤去电场,A将静止,此时B距C的左端距离为:l=d-xB=9.5m-8m=1.5m
则B刚滑上C的上表面时的速度为:vB″=$\sqrt{{v}_{B}^{′2}-2{a}_{2}l}$=$\sqrt{{4}^{2}-2×4×1.5}$m/s=2m/s
B与C在第一次与挡板P碰前的共同速度为:v0=$\frac{{m}_{B}{v}_{B}″}{{m}_{B}+{m}_{c}}$=$\frac{1×2}{1+0.5}$=$\frac{4}{3}$m/s
设木板C每次与P相碰后向左运动的最大距离分别为 s1、s2、s3…,第一次相碰后对C:
根据动能定理有:-μmBs1=0-$\frac{1}{2}{m}_{C}{v}_{0}^{2}$
解得:s1=$\frac{{m}_{C}{v}_{0}^{2}}{2μ{m}_{B}g}$=$\frac{0.5×(\frac{4}{3})^{2}}{2×0.4×1×10}$m=$\frac{1}{9}$m,
第一次碰,设B与C获得的共同速度为 v1,取水平向右为正方向,根据系统的动量守恒得:
(mB-mC)v0=(mB+mC)v1
解得:v1=$\frac{({m}_{B}-{m}_{C}){v}_{0}}{{m}_{B}+{m}_{C}}$
第二碰后,对C,由动能定理有:-μmgs2=0-$\frac{1}{2}{m}_{C}{v}_{1}^{2}$
解得:s2=$\frac{{m}_{C}{v}_{1}^{2}}{2μ{m}_{B}g}$=$(\frac{{m}_{B}-{m}_{C}}{{m}_{B}+{m}_{C}})^{2}$s1;
同理可得:s3=$(\frac{{m}_{B-}{m}_{C}}{{m}_{B}+{m}_{C}})^{4}{s}_{1}$;
…
所以,C与P相碰反弹后向左运动的最大距离均以q=$(\frac{{m}_{B}-{m}_{C}}{{m}_{B}+{m}_{C}})^{2}$=$\frac{1}{9}$的比例减小,C与P发生多次碰撞,所走的路程是一个无穷等比数列的和,公比为q,又C每次碰撞向左行的路程与向右行的路程相等,故C与P第一次碰撞后,木板C运动的总路程为:
s=2s1(1+q+q2+…)=$\frac{2{s}_{1}}{1-q}$=$\frac{2×\frac{1}{9}}{1-\frac{1}{9}}$m=0.25m.
答:(1)A与B第一次碰撞后B获得的速度是8m/s;
(2)A与B第二次碰撞后B获得的速度是4m/s;
(3)假设A与B完成第二次碰撞后的同时撤去电场,从C与P第一次碰撞后,木板C运动的总路程是0.25m.
点评 本题主要考查了牛顿第二定律、运动学基本公式、动量守恒定律的应用,并能运用数学归纳法和数列求和知识解题.


科目:高中物理 来源: 题型:解答题
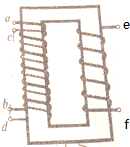 如图所示,一理想变压器的原、副线圈分别由双线圈ab和cd(匝数都为n1)及ef(匝数为n2)组成.
如图所示,一理想变压器的原、副线圈分别由双线圈ab和cd(匝数都为n1)及ef(匝数为n2)组成.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
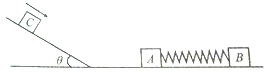 如图所示,木块A的质量为m,木块B的质量为km(k为常数),A,B由轻弹簧拴接,置于光滑水平面上,弹簧处于自然状态,一质量为m的木块C静止在木块A的左侧斜面上,木块C与斜面的动摩擦因数为μ=tanθ,斜面底端与木块A的距离足够长,现给木块C以初速度v0使之沿斜面向下运动,与A碰撞后,与A一起压缩弹簧,但与A不粘连.已知木块C返回斜面底端时的速度为$\frac{{v}_{0}}{2}$,最终静止在斜面上某处.设木块C的最大静摩擦力等于滑动摩擦力,不计木块经过斜面与平面连接处的能量损失,求:
如图所示,木块A的质量为m,木块B的质量为km(k为常数),A,B由轻弹簧拴接,置于光滑水平面上,弹簧处于自然状态,一质量为m的木块C静止在木块A的左侧斜面上,木块C与斜面的动摩擦因数为μ=tanθ,斜面底端与木块A的距离足够长,现给木块C以初速度v0使之沿斜面向下运动,与A碰撞后,与A一起压缩弹簧,但与A不粘连.已知木块C返回斜面底端时的速度为$\frac{{v}_{0}}{2}$,最终静止在斜面上某处.设木块C的最大静摩擦力等于滑动摩擦力,不计木块经过斜面与平面连接处的能量损失,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
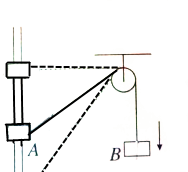 如图所示,套在竖直细杆上的环A跨过定滑轮且不可伸长的轻绳与重物B相连,由于B的质量较大,在释放B后,A将沿杆上升,当运动至定滑轮的连线处于水平位置时,其上升速度vA≠0,B未落地,这时B的速度为vB=0.
如图所示,套在竖直细杆上的环A跨过定滑轮且不可伸长的轻绳与重物B相连,由于B的质量较大,在释放B后,A将沿杆上升,当运动至定滑轮的连线处于水平位置时,其上升速度vA≠0,B未落地,这时B的速度为vB=0.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 图示时用于观察自感现象的电路图,图中线圈的自感系数很大,线圈的直流电阻RL与灯泡的电阻R满足RL<<R,则在开关S由闭合到断开的瞬间,可以观察到( )
图示时用于观察自感现象的电路图,图中线圈的自感系数很大,线圈的直流电阻RL与灯泡的电阻R满足RL<<R,则在开关S由闭合到断开的瞬间,可以观察到( )| A. | 灯泡A立即熄灭 | |
| B. | 灯泡B逐渐熄灭 | |
| C. | 灯泡A有明显的闪亮现象 | |
| D. | 只有在RL>>R时,才会看到灯泡A有明显的闪亮现象 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一质量m=0.5kg的金属杆在相距l=3m的水平轨道上与轨道垂直放置,固定住金属杆并在金属感中通以I=4A的恒定电流,如图所示,匀强磁场B垂直于轨道平面,磁感应强度的大小B=0.25T,金属杆与轨道间的动摩擦因数μ=0.2,取重力加速度g=10m/s2,
一质量m=0.5kg的金属杆在相距l=3m的水平轨道上与轨道垂直放置,固定住金属杆并在金属感中通以I=4A的恒定电流,如图所示,匀强磁场B垂直于轨道平面,磁感应强度的大小B=0.25T,金属杆与轨道间的动摩擦因数μ=0.2,取重力加速度g=10m/s2,查看答案和解析>>
科目:高中物理 来源: 题型:选择题
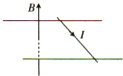
 两电阻R1,R2的伏安特性曲线如图所示,其中R1的图线与横轴的夹角为60°,R2的图线与横轴的夹角为30°,若将R1,R2串联起来接入电路中,则通电后R1,R2消耗的电功率之比为P1:P2等于( )
两电阻R1,R2的伏安特性曲线如图所示,其中R1的图线与横轴的夹角为60°,R2的图线与横轴的夹角为30°,若将R1,R2串联起来接入电路中,则通电后R1,R2消耗的电功率之比为P1:P2等于( )| A. | 1:$\sqrt{3}$ | B. | 3:$\sqrt{3}$ | C. | 1:3 | D. | 3:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,两质量分部均匀的球体半径分别为r1和r2,质量分别是m1和m2,且m1>m2,两球体内侧相距为r,则下列说法正确的是( )
如图,两质量分部均匀的球体半径分别为r1和r2,质量分别是m1和m2,且m1>m2,两球体内侧相距为r,则下列说法正确的是( )| A. | 两球间的万有引力大小为G$\frac{{m}_{1}{m}_{2}}{{r}^{2}}$ | |
| B. | 两球间的万有引力大小为G$\frac{{m}_{1}{m}_{2}}{({r}_{1}+{r}_{2}+r)^{2}}$ | |
| C. | m1对m2的引力大于m2对m1的引力 | |
| D. | m1与m2之间的引力总是大小相等、方向相反的,是一对平衡力 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com