
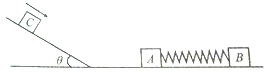
 如图所示,木块A的质量为m,木块B的质量为km(k为常数),A,B由轻弹簧拴接,置于光滑水平面上,弹簧处于自然状态,一质量为m的木块C静止在木块A的左侧斜面上,木块C与斜面的动摩擦因数为μ=tanθ,斜面底端与木块A的距离足够长,现给木块C以初速度v0使之沿斜面向下运动,与A碰撞后,与A一起压缩弹簧,但与A不粘连.已知木块C返回斜面底端时的速度为$\frac{{v}_{0}}{2}$,最终静止在斜面上某处.设木块C的最大静摩擦力等于滑动摩擦力,不计木块经过斜面与平面连接处的能量损失,求:
如图所示,木块A的质量为m,木块B的质量为km(k为常数),A,B由轻弹簧拴接,置于光滑水平面上,弹簧处于自然状态,一质量为m的木块C静止在木块A的左侧斜面上,木块C与斜面的动摩擦因数为μ=tanθ,斜面底端与木块A的距离足够长,现给木块C以初速度v0使之沿斜面向下运动,与A碰撞后,与A一起压缩弹簧,但与A不粘连.已知木块C返回斜面底端时的速度为$\frac{{v}_{0}}{2}$,最终静止在斜面上某处.设木块C的最大静摩擦力等于滑动摩擦力,不计木块经过斜面与平面连接处的能量损失,求:分析 (1)木块C返回斜面底端时的速度为$\frac{{v}_{0}}{2}$,对其上滑过程根据动能定理列式求解即可;
(2)木块C与斜面的动摩擦因数为μ=tanθ,木块C下滑过程中是匀速直线运动;C与A碰撞过程,C与A系统动量守恒,根据动量守恒定律列式求解碰撞后的共同速度;此后弹簧被压缩,B加速,A与C减速,当A、B、C速度相等时,弹簧被压缩到最大,弹性势能最大,根据动量守恒定律列式求解共同速度,根据能量守恒定律求解最大弹性势能;此后AC继续减速,B继续加速,当弹簧恢复原长时,A与C分离,根据能量守恒定律和动量守恒定律列式后联立求解,即可得到块A、C分离时木块B的速度;
(3)在木块A、C分离以后的过程中,A、B系统动量守恒,如果木块B的速度为零,根据动量守恒定律列式求解A的速度,结合能量守恒定律列式求解即可.
解答 解:(1)由于μ=tanθ,故木块C下滑过程中,滑动摩擦力与重力的下滑分力平衡,做匀速直线运动;
故与A碰撞前的速度为v0,反弹速度大小为$\frac{1}{2}{v}_{0}$,上滑过程,根据动能定理,有:
-(f+mgsinθ)L=0-$\frac{1}{2}m(\frac{{v}_{0}}{2})^{2}$
其中:
f=μmgcosθ=mgsinθ
故:L=$\frac{{v}_{0}^{2}}{16gsinθ}$
(2)C与A碰撞过程,C与A系统动量守恒,C与A碰撞过程时间极短,B的速度为零不变;
故:mv0=(m+m)v1
解得:${v}_{1}=\frac{{v}_{0}}{2}$
当AB速度相等时,弹簧的弹性势能最大,根据动量守恒定律,有:
mv0=(m+m+km)v
解得:v=$\frac{{v}_{0}}{2+k}$;
故最大弹性势能为:
Epm=$\frac{1}{2}(2m){v}_{1}^{2}$-$\frac{1}{2}(2m+km){v}^{2}$=$\frac{k}{4(2+k)}m{v}_{0}^{2}$
当弹簧第一次恢复原长时,AC分离,根据动量守恒定律,有:
mv0=m(-$\frac{{v}_{0}}{2}$)+mvA+kmvB ①
根据机械能守恒定律,有:
$\frac{1}{2}(2m){v}_{1}^{2}$=$\frac{1}{2}m(\frac{{v}_{0}}{2})^{2}$+$\frac{1}{2}m{v}_{A}^{2}+$$\frac{1}{2}km{v}_{B}^{2}$ ②
联立解得:
${v}_{B}=\frac{3k+\sqrt{2{k}^{2}-7}}{2({k}^{2}+1)}{v}_{0}$
或:${v}_{B}=\frac{3k-\sqrt{2{k}^{2}-7}}{2({k}^{2}+1)}{v}_{0}$
(3)在木块A、C分离以后的过程中,A、B系统动量守恒,如果B的速度为零,根据动量守恒定律,有:
mv0=m(-$\frac{{v}_{0}}{2}$)+mvA′+kmvB′
vB′=0
解得:vA′=$\frac{3}{2}{v}_{0}$
由于$\frac{1}{2}m{v}_{A}^{′2}$=$\frac{9}{8}m{v}_{0}^{2}$$>\frac{1}{2}m{v}_{0}^{2}$,即不符合能量守恒定律,故不可能出现B的速度为零的情况.
答:(1)木块C最终静止时距离斜面底端的距离为$\frac{{v}_{0}^{2}}{16gsinθ}$;
(2)弹簧弹性热能的最大值为$\frac{k}{4(2+k)}m{v}_{0}^{2}$,木块AC分离时木块B的速度为$\frac{3k+\sqrt{2{k}^{2}-7}}{2({k}^{2}+1)}{v}_{0}$ 或$\frac{3k-\sqrt{2{k}^{2}-7}}{2({k}^{2}+1)}{v}_{0}$;
(3)在木块AC分离以后的过程中,不管k取何值,木块B均不可能有速度为零的时刻.
点评 本题是典型的三多问题,即物体多、规律多、过程多,关键是分析清楚受力情况、运动情况和能量转化情况,多次结合动量守恒定律和功能关系列式分析后列式求解即可.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
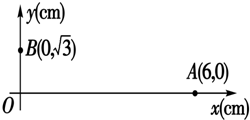 如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则
如图所示,在平面直角坐标系中,有方向平行于坐标平面的匀强电场,其中坐标原点O处的电势为0V,点A处的电势为6V,点B处的电势为3V,则查看答案和解析>>
科目:高中物理 来源: 题型:解答题
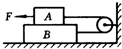 所受重力分别为G1和G2的滑块A,B,由绕过定滑轮的细绳相连后,叠放在水平桌面上,如图所示.已知A,B间的摩擦系数为μ1,B与桌面间的摩擦系数为μ2.问:
所受重力分别为G1和G2的滑块A,B,由绕过定滑轮的细绳相连后,叠放在水平桌面上,如图所示.已知A,B间的摩擦系数为μ1,B与桌面间的摩擦系数为μ2.问:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
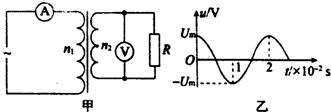
| A. | 通过R的电流iR随时间t的变化规律是iR=$\sqrt{2}$cos100πt(A) | |
| B. | 电压表V的示数为8V | |
| C. | 电流表A的示数为0.48A | |
| D. | 变压器的输入功率为8W |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
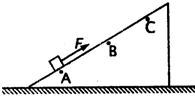 如图所示,一光滑斜面固定在水平地面上,质量m=1kg的物体在平行于斜面向上的恒力F作用下从A点由静止开始运动,到达B点时撤去拉力F,物体到达C点时速度为零.通过传感器测得每隔0.2s物体的瞬时速度如表.
如图所示,一光滑斜面固定在水平地面上,质量m=1kg的物体在平行于斜面向上的恒力F作用下从A点由静止开始运动,到达B点时撤去拉力F,物体到达C点时速度为零.通过传感器测得每隔0.2s物体的瞬时速度如表.| t/s | 0.0 | 0.2 | 0.4 | … | 2.2 | 2.4 | 2.6 | … |
| v/m•g-1 | 0.0 | 1.0 | 2.0 | … | 3.3 | 2.1 | 0.9 | … |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
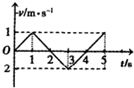
| A. | 第1s末质点速度方向将发生改变 | B. | 第2s质点的位移大小为2m | ||
| C. | 第3s内质点的速率逐渐减小 | D. | 第4s末质点的位置与起点时刻相同 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com