
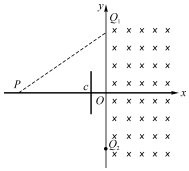
 如图所示的xOy坐标系中,y轴右侧空间存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直于xOy平面向里.P点的坐标为(-6L,0),Q1、Q2两点的坐标分别为(0,3L),(0,-3L).坐标为(-L,0)处的C点固定一平行于y轴放置一足够长的绝缘弹性挡板,带电粒子与弹性绝缘挡板碰撞前后,沿y方向分速度不变,沿x方向分速度反向,大小不变.带负电的粒子质量为m,电量为q,不计粒子所受重力.若粒子在P点沿PQ1方向进入磁场,经磁场运动后,求:
如图所示的xOy坐标系中,y轴右侧空间存在范围足够大的匀强磁场,磁感应强度大小为B,方向垂直于xOy平面向里.P点的坐标为(-6L,0),Q1、Q2两点的坐标分别为(0,3L),(0,-3L).坐标为(-L,0)处的C点固定一平行于y轴放置一足够长的绝缘弹性挡板,带电粒子与弹性绝缘挡板碰撞前后,沿y方向分速度不变,沿x方向分速度反向,大小不变.带负电的粒子质量为m,电量为q,不计粒子所受重力.若粒子在P点沿PQ1方向进入磁场,经磁场运动后,求:分析 (1)作出粒子运动的轨迹图,结合几何关系求出粒子在磁场中运动的轨道半径,根据半径公式求出粒子的速度.
(2)粒子进入磁场后做周期性运动,分析粒子一个周期的运动情况,根据几何关系以及对称性.即可求出粒子经过坐标原点O之后再回到P点所满足的关系式;
(3)粒子与挡板碰撞三次并能回到P点,作出轨迹图,结合几何关系,运用半径公式进行求解.
解答  解:(1)粒子与挡板只碰撞一次,粒子运动的轨迹如图一所示,粒子运动的轨道半径为R,碰撞前后出入磁场两点之间的距离为L
解:(1)粒子与挡板只碰撞一次,粒子运动的轨迹如图一所示,粒子运动的轨道半径为R,碰撞前后出入磁场两点之间的距离为L
则:根据几何关系可得:4Rcosθ-L=6L,其中:cosθ=$\frac{2\sqrt{5}}{5}$
解得:R=$\frac{7\sqrt{5}L}{8}$ ①
根据半径公式:R=$\frac{mv}{qB}$ ②
联立①②式可得:v=$\frac{7\sqrt{5}qBL}{8m}$
(2)设粒子在x轴上方与挡板碰撞n次,
每次圆周运动,粒子位置沿y轴向下平移的距离为2Rcosθ,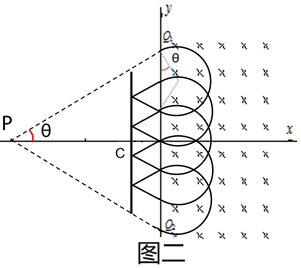
与挡板相碰后,粒子位置向上平移的距离为L,
一次周期性运动粒子沿y轴共向下平移为2Rcosθ-L,
要使粒子经过坐标原点O之后再回到P点需满足:
(n-1)(2Rcosθ-L)+2Rcosθ=3L (n=2,3,4…) ③
联立②③式子可得:v=$\frac{(n+2)qBL}{2nmcosθ}$ (n=2,3,4…)
所以,只要粒子速度满足v=$\frac{(n+2)qBL}{2nmcosθ}$ (n=2,3,4…)粒子就可以经过坐标原点O之后再回到P点(图二为n=2时的过程图)
(3)若与挡板碰撞三次,如图二所示,设挡板的长度L0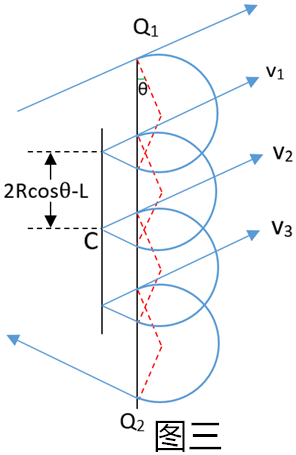
根据几何关系可得:3(2Rcosθ-L)+2Rcosθ=6L
解得:R=$\frac{9\sqrt{5}L}{16}$ ④
根据半径公式:R=$\frac{mv}{qB}$可得:v=$\frac{9\sqrt{5}qBL}{16m}$ ⑤
联立④⑤式子可得:挡板的长度的最小值L0=2(2Rcosθ-L)=2.5L
答:(1)只与挡板碰撞一次并能回到P点的粒子初速度大小为$\frac{7\sqrt{5}qBL}{8m}$;
(2)粒子能经过坐标原点O之后再回到P点;
(3)只与挡板碰撞三次并能回到P点的粒子初速度大小以及这种情况下挡板的长度至少为2.5L.
点评 本题考查带电粒子在磁场中的运动,第二问为多次回旋的周期性运动,分析每次周期性运动粒子位置变化情况,注意利用几何关系和对称性去分析;对于第一问和第三问,解题关键是要做出粒子的轨迹图,运用半径公式结合几何关系进行求解.


科目:高中物理 来源: 题型:多选题
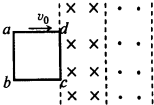 如图所示,边长为L、总电阻为R的均匀正方形线框abcd放置在光滑水平桌面上,其cd边右侧紧邻两个磁感应强度为B、宽度为L、方向相反的有界匀强磁场.现使线框以速度v0匀速通过磁场区域,从开始进入,到完全离开磁场的过程中,下列图线能定性反映线框中的感应电流(以逆针方向为正)和a、b两点间的电势差随时间变化关系的是( )
如图所示,边长为L、总电阻为R的均匀正方形线框abcd放置在光滑水平桌面上,其cd边右侧紧邻两个磁感应强度为B、宽度为L、方向相反的有界匀强磁场.现使线框以速度v0匀速通过磁场区域,从开始进入,到完全离开磁场的过程中,下列图线能定性反映线框中的感应电流(以逆针方向为正)和a、b两点间的电势差随时间变化关系的是( )| A. | 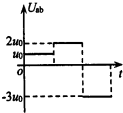 | B. | 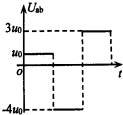 | C. | 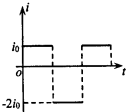 | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,两足够长的光滑金属导轨竖直放置,相距L=1 m,一理想电流表和一电阻R=10Ω的电阻通过导线与两导轨相连,导轨之间存在着方向相同、高度均为h的匀强磁场Ⅰ、Ⅱ,匀强磁场与导轨平面垂直.一质量为m=1 kg、有效电阻也为R=10Ω的导体棒,从距磁场Ⅰ下方边界一定距离处,在F=20 N的恒定外力作用下从静止开始竖直向上运动,导体棒在Ⅰ磁场中运动的过程中电流表的示数恒为1 A,导体棒离开磁场Ⅱ前的一段时间内电流表的示数恒为2 A,导体棒始终保持水平,不计导轨的电阻.(g=10 m/s2).求:
如图所示,两足够长的光滑金属导轨竖直放置,相距L=1 m,一理想电流表和一电阻R=10Ω的电阻通过导线与两导轨相连,导轨之间存在着方向相同、高度均为h的匀强磁场Ⅰ、Ⅱ,匀强磁场与导轨平面垂直.一质量为m=1 kg、有效电阻也为R=10Ω的导体棒,从距磁场Ⅰ下方边界一定距离处,在F=20 N的恒定外力作用下从静止开始竖直向上运动,导体棒在Ⅰ磁场中运动的过程中电流表的示数恒为1 A,导体棒离开磁场Ⅱ前的一段时间内电流表的示数恒为2 A,导体棒始终保持水平,不计导轨的电阻.(g=10 m/s2).求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
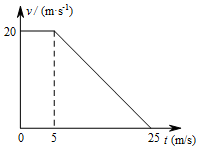 一辆客车正在以v1=20m/s的速度匀速行驶,突然,司机看见正前方x=65m(距车队队尾)处有一列汽车车队以8m/s的速度正在匀速行驶,相邻汽车间距为20m,客车司机立即采取制动措施.若从司机看见车队开始计时(t=0),客车的速度-时间图象如图所示(汽车和客车大小不计).
一辆客车正在以v1=20m/s的速度匀速行驶,突然,司机看见正前方x=65m(距车队队尾)处有一列汽车车队以8m/s的速度正在匀速行驶,相邻汽车间距为20m,客车司机立即采取制动措施.若从司机看见车队开始计时(t=0),客车的速度-时间图象如图所示(汽车和客车大小不计).查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 原子核的结合能等于使其完全分解成自由核子所需的最小能量 | |
| B. | 原子核的比结合能越大,表明组成原子核的核子数越大,原子核就越稳定 | |
| C. | 核燃料要用比结合能小的核 | |
| D. | ${\;}_{94}^{239}Pu$衰变成α粒子和${\;}_{92}^{235}U$,α粒子和${\;}_{92}^{235}U$的质量之和一定小于${\;}_{94}^{239}Pu$的质量 | |
| E. | 氕和氚结合成氦原子核,其质量亏损所对应的能量等于该氦原子核的结合能 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
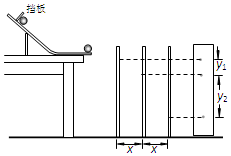 在做“研究平抛运动”的实验中,为了确定小球在不同时刻所通过的位置,实验时用如图所示的装置.实验操作的主要步骤如下:
在做“研究平抛运动”的实验中,为了确定小球在不同时刻所通过的位置,实验时用如图所示的装置.实验操作的主要步骤如下:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 麦克斯韦首先预言了电磁波的存在,赫兹通过实验加以了证实 | |
| B. | 奥斯特发现了通电导体在磁场中受力规律 | |
| C. | 托马斯﹒杨的双缝干涉实验证明了光具有波动性 | |
| D. | 法拉第发现了电磁感应现象 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com