
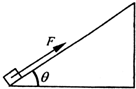
 已知足够长的斜面倾角θ=37°,质量m=l0kg的物体,在斜面底部受到沿斜面向上的力F=100N作用,由静止开始运动,物体在前2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:
已知足够长的斜面倾角θ=37°,质量m=l0kg的物体,在斜面底部受到沿斜面向上的力F=100N作用,由静止开始运动,物体在前2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求: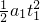 得
得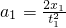 =2m/s2
=2m/s2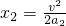 =1m
=1m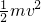 .
. 

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中物理 来源: 题型:
 已知足够长的斜面倾角θ=37°,质量m=l0kg的物体,在斜面底部受到沿斜面向上的力F=100N作用,由静止开始运动,物体在前2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:
已知足够长的斜面倾角θ=37°,质量m=l0kg的物体,在斜面底部受到沿斜面向上的力F=100N作用,由静止开始运动,物体在前2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:
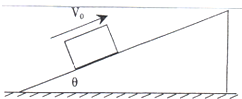 如图所示,足够长的斜面倾角θ=37°,一个物体以v0=12/s的初速度,从斜面A点处沿斜面向上运动.加速度大小为a=8.0m/s2,已知重力加速度g=10m/s2 (sin37°=0.6,cos37°=0.8.)求:
如图所示,足够长的斜面倾角θ=37°,一个物体以v0=12/s的初速度,从斜面A点处沿斜面向上运动.加速度大小为a=8.0m/s2,已知重力加速度g=10m/s2 (sin37°=0.6,cos37°=0.8.)求:查看答案和解析>>
科目:高中物理 来源: 题型:
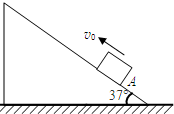 如图,足够长的斜面倾角θ=37°.一个物体以v0=12m/s的初速度从斜面A点处沿斜面向上运动.物体与斜面间的动摩擦因数为μ=0.25.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:
如图,足够长的斜面倾角θ=37°.一个物体以v0=12m/s的初速度从斜面A点处沿斜面向上运动.物体与斜面间的动摩擦因数为μ=0.25.已知重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:查看答案和解析>>
科目:高中物理 来源:2011年山东省枣庄八中高考物理一模试卷(解析版) 题型:解答题
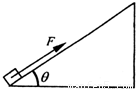 已知足够长的斜面倾角θ=37°,质量m=l0kg的物体,在斜面底部受到沿斜面向上的力F=100N作用,由静止开始运动,物体在前2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:
已知足够长的斜面倾角θ=37°,质量m=l0kg的物体,在斜面底部受到沿斜面向上的力F=100N作用,由静止开始运动,物体在前2s内位移为4m,2s末撤掉力F,(sin37°=0.6,cos37°=0.8,取g=10m/s2)求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com