Question

一列货车以v₁=28.8km/h的速度在平直铁路上运行.由于调度事故，在大雾中后面相距s₀= 600m处有一列客车以v₂=72km/h的速度在同一铁轨上驶来.客车司机发现货车后立即紧急制动，为不使两车相撞，客车的制动加速度至少多大？设货车速度不变.

Answer 1

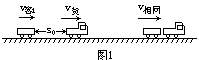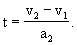
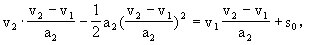
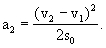
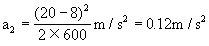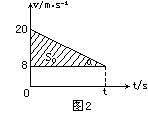
　[分析]这里有两个研究对象：货车与客车.货车始终以v₁做匀速直线运动，客车以v₂为初速作匀减速运动.不致相撞时，客车和货车应同时满足位移条件（s_客≤s_货）和速度条件（v_客≤v_货）.如图1.　　[解]以车行方向为正方向，设客车制动后的加速度大小为a₂.由上述不相撞的条件得　　　　当制动加速度取最小值时，两个不等式可改为等式.由（2）式得客车速度减小到等于货车速度的时间　　代入（1）式，得　　　　整理后得　　　　以v₁=28.8km/h=8m/s，v₂=72km/h=20m/s，s₀=600m代入得　　　　[说明] 本题也可用v－t图求解.如图2所示，画出两车的速度图线.刚好相遇不相撞时，其中画有斜线的三角形面积数值上应等于s₀，即

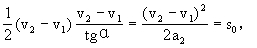
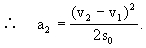
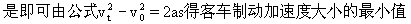
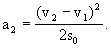
　　上面的计算都是以地面为参照物的.如果改以货车为参照物，即站在货车上看后方的客车，客车制动后相对于它以初速（v₂-v₁）、加速度a₂向它驶来，不相撞时，经位移s₀后恰好静止（即与货车相对静止）.于　　必须注意，相遇（追及）和相遇不相撞两者的物理条件不同.相遇时只需满足一个位移条件（例2）；相遇不相撞还需同时满足速度条件，即后车的速度应不大于前车的速度，临界情况下两车速度相等.