
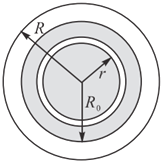
 �趨������һ���������ȷֲ������壬��֪�����ֲ����ȵ���Ƕ����ڲ����������Ϊ�㣮��ͼ��ʾ���п�ѧ�������ڵ����ڲ���һ���뾶Ϊr�Ļ��ι�����ڻ��ι���ڷ���һ�����조���ǡ�A�����조���ǡ�������������������������Բ���˶������ڵ����Ͽշ���һ�Ź���뾶ΪR�������������B����֪����뾶ΪRo�������й��ڡ����ǡ�A������B�˶������ļ��ٶȴ�С�����ٶȴ�С�����ٶȡ�����֮����ȷ���ǣ�������
�趨������һ���������ȷֲ������壬��֪�����ֲ����ȵ���Ƕ����ڲ����������Ϊ�㣮��ͼ��ʾ���п�ѧ�������ڵ����ڲ���һ���뾶Ϊr�Ļ��ι�����ڻ��ι���ڷ���һ�����조���ǡ�A�����조���ǡ�������������������������Բ���˶������ڵ����Ͽշ���һ�Ź���뾶ΪR�������������B����֪����뾶ΪRo�������й��ڡ����ǡ�A������B�˶������ļ��ٶȴ�С�����ٶȴ�С�����ٶȡ�����֮����ȷ���ǣ�������| A�� | $\frac{{a}_{A}}{{a}_{B}}$=��$\frac{R}{r}$��2 | B�� | $\frac{{v}_{A}}{{v}_{B}}$=$\frac{r}{{R}_{0}}$$\sqrt{\frac{R}{{R}_{0}}}$ | C�� | $\frac{{��}_{A}}{{��}_{B}}$=$\frac{R}{{R}_{0}}$$\sqrt{\frac{R}{{R}_{0}}}$ | D�� | $\frac{{T}_{A}}{{T}_{B}}$=$\frac{R}{r}$$\sqrt{\frac{R}{r}}$ |
���� �ɵ������������ܶȳ���������ɵõ�����������ʽ�������������ṩ����������A��B�ֱ��з��̿ɵ��������������֮�ȣ�
��� �⣺�������ܶ�Ϊ�ѣ����ڵ���A��$G\frac{��\frac{4}{3}��{r}^{3}}{{r}^{2}}=\frac{{v}_{A}^{2}}{r}={a}_{A}=r{��}_{A}^{2}$��
��������B��$G\frac{��\frac{4}{3}��{R}_{0}^{3}}{{R}^{2}}=\frac{{v}_{B}^{2}}{R}={a}_{B}=R{��}_{B}^{2}$=R$\frac{4{��}^{2}}{{T}_{B}^{2}}$
��ã�A��$\frac{{a}_{A}}{{a}_{B}}$=$\frac{{R}^{2}r}{{R}_{0}^{2}}$����A����
B��$\frac{{v}_{A}}{{v}_{B}}=\frac{r}{{R}_{0}}\sqrt{\frac{R}{{R}_{0}}}$����B��ȷ
C��$\frac{{��}_{A}}{{��}_{B}}$=$\frac{R}{{R}_{0}}\sqrt{\frac{R}{{R}_{0}}}$����C��ȷ
������D��$\frac{{T}_{A}}{{T}_{B}}=\frac{{R}_{0}}{R}\sqrt{\frac{{R}_{0}}{R}}$����D����
��ѡ��BC
���� �ɵ������������ܶȳ���������ɵõ�����������ʽ�������������ṩ����������A��B�ֱ��з��̿ɵ��������ٶȺͼ��ٶ�֮�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ��ͼ��ʾ��ijͬѧΪ��֤���ܶ����������ͼ��ʾ��ʵ�飬��Ƥ��̶������ӵ��Ҷˣ�һ����Ϊm��С���̶�����Ƥ���ϣ�С����Oλ��ʱ��Ƥ��ǡ�ô���ԭ������ȫ��ͬ����Ƥ���������Ը�����Aλ��Ϊ����ţ�С���ϵ���Ŀ���ΪD��OA��ľ���ΪL�����������̵�������ΪM��С����������Ħ�����Բ��ƣ�
��ͼ��ʾ��ijͬѧΪ��֤���ܶ����������ͼ��ʾ��ʵ�飬��Ƥ��̶������ӵ��Ҷˣ�һ����Ϊm��С���̶�����Ƥ���ϣ�С����Oλ��ʱ��Ƥ��ǡ�ô���ԭ������ȫ��ͬ����Ƥ���������Ը�����Aλ��Ϊ����ţ�С���ϵ���Ŀ���ΪD��OA��ľ���ΪL�����������̵�������ΪM��С����������Ħ�����Բ��ƣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�����浼��Ļ����ϰ�װ�˿���Ϊd���ڹ�壬�������˶��Ļ����Ⱥ�ͨ����������ţ����ֺ���Ƽ�¼���ڹ��ͨ����һ������ŵ�ʱ��Ϊt1��ͨ���ڶ�������ŵ�ʱ��Ϊt2���ڹ��ӿ�ʼ��ס��һ������ŵ���ʼ��ס�ڶ�������ŵ�ʱ��Ϊ��t�����в����������ӽ���ʵֵ���ǣ�������
��ͼ��ʾ�����浼��Ļ����ϰ�װ�˿���Ϊd���ڹ�壬�������˶��Ļ����Ⱥ�ͨ����������ţ����ֺ���Ƽ�¼���ڹ��ͨ����һ������ŵ�ʱ��Ϊt1��ͨ���ڶ�������ŵ�ʱ��Ϊt2���ڹ��ӿ�ʼ��ס��һ������ŵ���ʼ��ס�ڶ�������ŵ�ʱ��Ϊ��t�����в����������ӽ���ʵֵ���ǣ�������| A�� | �����˶��ļ��ٶ�Ϊ$\frac{{d��{t_1}-{t_2}��}}{{{t_1}{t_2}����t��}}$ | |
| B�� | �����˶��ļ��ٶ�Ϊ$\frac{{2d��{t_1}-{t_2}��}}{{{t_1}{t_2}[{2����t��+{t_2}-{t_1}}]}}$ | |
| C�� | �ڹ���е�ͨ����һ������ŵ��ٶ�Ϊ$\frac{d}{t_1}$ | |
| D�� | �ڹ��ǰ��ͨ����һ������ŵ��ٶ�Ϊ$\frac{d}{t_1}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
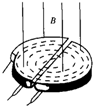 �����������ǻ�ø��ܴ������ӵ�װ�ã�����IJ����Ƿֱ����Ƶ������Դ����������������D�κУ����м���������γ������Ա仯�ĵ糡��ʹ������ͨ������ʱ���ܵõ����٣���D�ν����д��ڴ�ֱ�ںе���ǿ�ų��У���ͼ��ʾ�����ڻ���������������˵����ȷ���ǣ�������
�����������ǻ�ø��ܴ������ӵ�װ�ã�����IJ����Ƿֱ����Ƶ������Դ����������������D�κУ����м���������γ������Ա仯�ĵ糡��ʹ������ͨ������ʱ���ܵõ����٣���D�ν����д��ڴ�ֱ�ںе���ǿ�ų��У���ͼ��ʾ�����ڻ���������������˵����ȷ���ǣ�������| A�� | �������Ӵ�D�κ����ʱ�Ķ�������ٵ�ѹ�� | |
| B�� | �������Ӵ�D�κ����ʱ�Ķ�����ų���ǿ���й� | |
| C�� | ����������һ��Բ���˶���Ҫ���������Σ���˽���糡������ӦΪԲ���˶����ڵĶ��� | |
| D�� | ��ͬһ�����������ֱ���ٲ�ͬ�Ĵ������ӣ����õ��ڽ���糡��Ƶ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
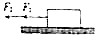 ��ͼ��ʾ��һ�ʵ㾲ֹ�ڹ⻬ˮƽ���ϣ���ijʱ�̿�ʼͬʱ�ܵ�����ˮƽ�������F1��F2���ã�F1��F2�����ʵ��˶������෴������F1�Ĺ��ʲ��䣬��СΪP��F2=kv��kΪ����ϵ����vΪ�ʵ��˲ʱ�ٶȣ������ʵ����Ժ��˶������У����ٶȴ�С�Ŀ���Ϊ��������
��ͼ��ʾ��һ�ʵ㾲ֹ�ڹ⻬ˮƽ���ϣ���ijʱ�̿�ʼͬʱ�ܵ�����ˮƽ�������F1��F2���ã�F1��F2�����ʵ��˶������෴������F1�Ĺ��ʲ��䣬��СΪP��F2=kv��kΪ����ϵ����vΪ�ʵ��˲ʱ�ٶȣ������ʵ����Ժ��˶������У����ٶȴ�С�Ŀ���Ϊ��������| A�� | $\frac{\sqrt{Pk}}{2m}$ | B�� | $\frac{\sqrt{Pk}}{m}$ | C�� | $\frac{3\sqrt{Pk}}{m}$ | D�� | $\frac{4\sqrt{Pk}}{m}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
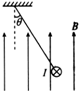 һ��L=0.5m������m=0.2kg��ˮƽֱ����ͨ����Եϸ���������컨���ϣ�����װ�ô��ڷ�����ֱ���ϵ���ǿ�ų�B�У���������ͨ�Դ�ֱ��ֽ�������СΪI=10A�ĵ������õ��߾�ֹʱϸ������ֱ�����ļнǦ�=37�㣬��ͼ��ʾ���ֱ��ִŸ�Ӧǿ�ȵĴ�С���䣬�ôų�������ֽ��������ʱ�뷽����ת��90�㣬ȡ�������ٶ�g=10m/s2����֪sin37��=0.6��������˵������ȷ���У�������
һ��L=0.5m������m=0.2kg��ˮƽֱ����ͨ����Եϸ���������컨���ϣ�����װ�ô��ڷ�����ֱ���ϵ���ǿ�ų�B�У���������ͨ�Դ�ֱ��ֽ�������СΪI=10A�ĵ������õ��߾�ֹʱϸ������ֱ�����ļнǦ�=37�㣬��ͼ��ʾ���ֱ��ִŸ�Ӧǿ�ȵĴ�С���䣬�ôų�������ֽ��������ʱ�뷽����ת��90�㣬ȡ�������ٶ�g=10m/s2����֪sin37��=0.6��������˵������ȷ���У�������| A�� | �ų�δת��ʱ����Եϸ�߶�ͨ�絼�ߵ�������СΪ2.5N | |
| B�� | �ôų��ĴŸ�Ӧǿ�ȴ�СΪ1.5T | |
| C�� | ת�������о�Եϸ������ֱ����ļн��ȱ����С | |
| D�� | ת�������о�Եϸ���ܵ���������СֵΪ1.6N |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
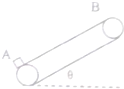 �������ˮ���ϰ�װ�д��ʹ����ô��ʹ������������Դ����߹���Ч�ʣ����ʹ��Ժ㶨������v=2m/s��������Ϊm=0.5kg�Ĺ�����������Aλ�÷ŵ����ʹ��ϣ����ij��ٶȺ��Բ��ƣ������봫�ʹ�֮��Ķ�Ħ������$��=\frac{\sqrt{3}}{2}$�����ʹ���ˮƽ����н��Ǧ�=30�㣬���ʹ�AB������l=16.8m��ÿ��ǰһ�������ڴ��ʹ���ֹͣ��Ի���ʱ��һ�����������ŵ����ʹ��ϣ�ȡg=10m/s2����
�������ˮ���ϰ�װ�д��ʹ����ô��ʹ������������Դ����߹���Ч�ʣ����ʹ��Ժ㶨������v=2m/s��������Ϊm=0.5kg�Ĺ�����������Aλ�÷ŵ����ʹ��ϣ����ij��ٶȺ��Բ��ƣ������봫�ʹ�֮��Ķ�Ħ������$��=\frac{\sqrt{3}}{2}$�����ʹ���ˮƽ����н��Ǧ�=30�㣬���ʹ�AB������l=16.8m��ÿ��ǰһ�������ڴ��ʹ���ֹͣ��Ի���ʱ��һ�����������ŵ����ʹ��ϣ�ȡg=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
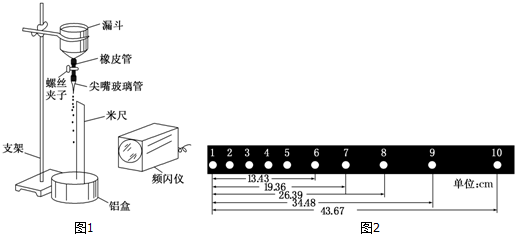
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com