
分析 抓住双星模型转动的周期相等,根据万有引力提供向心力求出周期与总质量和两星之间距离的关系,从而得出周期的变化.
解答 解:对恒星m1:$G\frac{{{m_1}{m_2}}}{L^2}={m_1}\frac{{4{π^2}}}{T^2}{r_1}$
对恒星m2:$G\frac{{{m_1}{m_2}}}{L^2}={m_2}\frac{{4{π^2}}}{T^2}{r_2}$
距离关系有:L=r1+r2,
由以上三式得:$T=\sqrt{\frac{{4{π^2}{L^3}}}{{G{M_总}}}}$
设经过一段时间演化后,两星总质量变为原来的k倍,两星之间的距离变为原来的n倍,则此时圆周运动的周期为:
T′=2π$\sqrt{\frac{(nL)^{3}}{G(kM)}}$=$\sqrt{\frac{n^3}{k}}$T.
将k=1.2,n=1.8代入上式得:T′=$\sqrt{\frac{1.{8}^{3}}{1.2}}T$=$\sqrt{4.86}T$≈2.2T
答:此时圆周运动的周期为2.2T.
点评 解决本题的关键知道双星模型靠相互间的万有引力提供向心力,角速度相等,周期相等,结合万有引力提供向心力进行求解.


科目:高中物理 来源: 题型:实验题
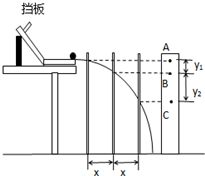 在做“研究平抛物体的运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面,并垂直于斜槽末端部分所在直线;使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板上并在白纸上留下痕迹A;将木板向远离槽口平移一段距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板上得到痕迹B;又将木板向远离槽口平移一段距离x,小球再从斜槽上紧靠挡板处由静止释放,小球撞到木板上得到痕迹C.若测得木板每次移动的距离x=15.00cm,A、B间的距离y1=15.00cm,B、C间的距离y2=25.00cm.(g取10m/s2).回答下列问题:
在做“研究平抛物体的运动”的实验中,为了确定小球在不同时刻在空中所通过的位置,实验时用了如图所示的装置.先将斜槽末端调整水平,在一块平整的木板表面钉上白纸和复写纸.将该木板竖直立于水平地面,并垂直于斜槽末端部分所在直线;使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板上并在白纸上留下痕迹A;将木板向远离槽口平移一段距离x,再使小球从斜槽上紧靠挡板处由静止释放,小球撞到木板上得到痕迹B;又将木板向远离槽口平移一段距离x,小球再从斜槽上紧靠挡板处由静止释放,小球撞到木板上得到痕迹C.若测得木板每次移动的距离x=15.00cm,A、B间的距离y1=15.00cm,B、C间的距离y2=25.00cm.(g取10m/s2).回答下列问题:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 质点的是路程矢量,位移是标量 | |
| B. | 质点通过的路程可以不等,但位移可能相同 | |
| C. | 质点通过的路程不为零,但位移可能是零 | |
| D. | 质点做直线运动时,它通过的路程就是位移大小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 伽利略通过对吊灯的观察,发现了吊灯摆动的等时性,并发明了摆钟 | |
| B. | 伽利略认为空中下落的物体,重的比轻的下落快 | |
| C. | 质点、自由落体运动都是理想化模型 | |
| D. | 研究物体运动只能以地面为参考系 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,A、B两个可看成是质点的两汽车沿同一直线运动,最初相距s0=17m,且A做初速度vA=6m/s、加速度为aA=2m/s2匀加速运动,B做初速度为vB=10m/s,以5m/s2的加速度作匀减速直线运动,求:
如图所示,A、B两个可看成是质点的两汽车沿同一直线运动,最初相距s0=17m,且A做初速度vA=6m/s、加速度为aA=2m/s2匀加速运动,B做初速度为vB=10m/s,以5m/s2的加速度作匀减速直线运动,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
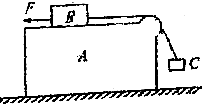 有一个带圆弧形凸起的长方形木块A固定在水平面上,木块A上的物体B用绕过凸起部分的轻绳与物体C相连,B与凸起之间的绳是水平的,有一水平向左边的拉力F作用在一物体B上,如果物体B、C均保持静止并且凸起部分下边与C物体相连的轻绳与竖直方向的夹角θ=37°,必须在C上加一水平向右的力Fx(图中没有画出)如图所示.己知物体B、C的质量均为m,物体B与木块A之间的动摩擦因数为μ,重力加速度为g,不计圆弧形凸起部分的摩擦,则拉力F在什么取值范围内才能使B静止?(设最大静摩擦力等于滑动摩擦力,sin37°=0.6)
有一个带圆弧形凸起的长方形木块A固定在水平面上,木块A上的物体B用绕过凸起部分的轻绳与物体C相连,B与凸起之间的绳是水平的,有一水平向左边的拉力F作用在一物体B上,如果物体B、C均保持静止并且凸起部分下边与C物体相连的轻绳与竖直方向的夹角θ=37°,必须在C上加一水平向右的力Fx(图中没有画出)如图所示.己知物体B、C的质量均为m,物体B与木块A之间的动摩擦因数为μ,重力加速度为g,不计圆弧形凸起部分的摩擦,则拉力F在什么取值范围内才能使B静止?(设最大静摩擦力等于滑动摩擦力,sin37°=0.6)查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 如图为验证机械能守恒定律的实验装置示意图.现有的器材:带铁夹的铁架台、电火花打点计时器、纸带、带夹子的重锤、天平.回答下列问题:
如图为验证机械能守恒定律的实验装置示意图.现有的器材:带铁夹的铁架台、电火花打点计时器、纸带、带夹子的重锤、天平.回答下列问题:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
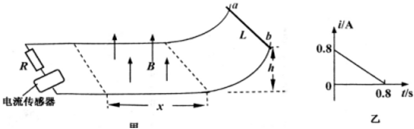 如图甲所示,两相距L=1m的光滑平行导轨,由水平和曲轨两部分平滑对接而成,导轨左端与电流传感器、定值电阻R=3Ω相连,两导轨间长x=1.6m的区域内存放一竖直方向的磁场.现使金属棒ab从距水平面高h=0.8m处的曲轨上释放,在进入水平轨道前的0.5s内磁感应强度B从-1T随时间均匀变化到+1T,后保持1T不变.棒ab进入水平轨道立刻施加一与棒垂直的水平外力.已知金属棒的质量m=0.2kg,电阻r=2Ω,不计导轨电阻及电流传感器对电路的影响.求:
如图甲所示,两相距L=1m的光滑平行导轨,由水平和曲轨两部分平滑对接而成,导轨左端与电流传感器、定值电阻R=3Ω相连,两导轨间长x=1.6m的区域内存放一竖直方向的磁场.现使金属棒ab从距水平面高h=0.8m处的曲轨上释放,在进入水平轨道前的0.5s内磁感应强度B从-1T随时间均匀变化到+1T,后保持1T不变.棒ab进入水平轨道立刻施加一与棒垂直的水平外力.已知金属棒的质量m=0.2kg,电阻r=2Ω,不计导轨电阻及电流传感器对电路的影响.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com