
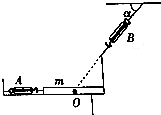
 ��ͼ��ʾ������Ϊm����ΪL���Ҷ���һ��ֱ��֧�ܵľ��ȳ�ľ��ƽ���������ϣ������֮һ�������ھ�ֹ״̬���ֱַ����ᵯ�ɳ�A��Bͨ��ϸ���볤ľ����������֪��ľ����ˮƽ�����Ķ�Ħ��������=0.6����=60�㣬�����Ħ�������ڻ���Ħ��������
��ͼ��ʾ������Ϊm����ΪL���Ҷ���һ��ֱ��֧�ܵľ��ȳ�ľ��ƽ���������ϣ������֮һ�������ھ�ֹ״̬���ֱַ����ᵯ�ɳ�A��Bͨ��ϸ���볤ľ����������֪��ľ����ˮƽ�����Ķ�Ħ��������=0.6����=60�㣬�����Ħ�������ڻ���Ħ������������ ��1��ľ�崦��ƽ��״̬�������������������жϣ�
��2��ľ�崦��ƽ��״̬��������������������ƽ�⼴�����
��3���ڼ���˲�䣬�жϳ�A���ɵĵ��������Ħ������Ĺ�ϵ�������жϳ�ľ���ܵ���Ħ�����Ĵ�С
��� �⣺��1��A��B���ɳ�ʾ����Ϊ��ʱ����ľ������������֪������ֱ����FN1-mg=0����FN1=mg
��2����ľ������������֪������ֱ����FNBsin��-mg=0
ˮƽ����FNA-FNBcos��=0
�������FNB=$\frac{mg}{sin��}$=$\frac{2\sqrt{3}mg}{3}$
${F}_{NA}=\frac{mg}{tan��}$=$\frac{\sqrt{3}mg}{3}$
��3��ľ���ܵ������Ħ����f=��mg=0.6mg$��\frac{\sqrt{3}mg}{3}$���ʼ���˲�䣬ľ�屣�־�ֹ����ʱ�ܵ���Ħ����Ϊ��Ħ������СΪf=$\frac{\sqrt{3}mg}{3}$
�𣺣�1��A��B���ɳ�ʾ����Ϊ��ʱ������Գ�ľ���֧�����Ĵ�СΪmg��
��2����ľ��������ѹ��Ϊ��ʱ��AB�����ɳӵ�ʾ��Ϊ�ֱ�Ϊ$\frac{\sqrt{3}mg}{3}$��$\frac{2\sqrt{3}mg}{3}$
��3���ڣ�2�������У�֧���϶�����B���ɳӵ�ϸ��ͻȻ���ѣ�ľ���ܵ���Ħ�����Ĵ�СΪ$\frac{\sqrt{3}mg}{3}$
���� ������Ҫ�����˹����������µ�ƽ�⣬�ؼ�ʱ������������ȷ�жϳ�A���ɵĵ�����Сԡ���Ħ������Ĺ�ϵʱ��������ʵĹؼ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
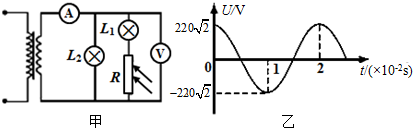
| A�� | �ý����������T=2s | |
| B�� | ��ѹ����ʾ��Ϊ55$\sqrt{2}$V | |
| C�� | ��������������R�Ĺ���ǿ�ȣ���ԭ��Ȧ���빦�ʼ�С | |
| D�� | ��������������R�Ĺ���ǿ�ȣ���L1�䰵��L2������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
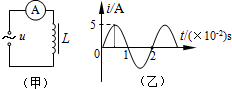 ��ͼ����ʾ��·�У����ΪL����Ȧ�������A��������ڽ�����Դ�ϣ�����·��ͨ����ͼ����ʾ����ʽ�������ʱ������˵������ȷ���ǣ�������
��ͼ����ʾ��·�У����ΪL����Ȧ�������A��������ڽ�����Դ�ϣ�����·��ͨ����ͼ����ʾ����ʽ�������ʱ������˵������ȷ���ǣ�������| A�� | ����������Ϊ5A | |
| B�� | LԽ��жԽ������谭����Խ�� | |
| C�� | t=2��10-2sʱ����Ȧ�е��Ըе綯����С | |
| D�� | t=2��10-2sʱ����Ȧ�е����Ĵų���ǿ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
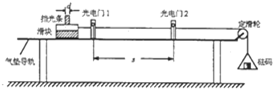 ��ͼ��ʾ�����������浼�조��֤��е���غ㶨�ɡ���ʵ��װ�ã������ڸõ������˶�ʱ���������ɺ��ԣ�
��ͼ��ʾ�����������浼�조��֤��е���غ㶨�ɡ���ʵ��װ�ã������ڸõ������˶�ʱ���������ɺ��ԣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
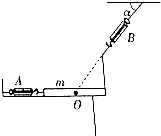 ��ͼ��ʾ������Ϊm����ΪL���Ҷ���һ��ֱ��֧�ܵľ��ȳ�ľ��ƽ���������ϣ������֮һ�������ھ�ֹ״̬���ֱַ����ᵯ�ɳ�A��Bͨ��ϸ���볤ľ����������֪��ľ����ˮƽ�����Ķ�Ħ��������=0.6����=60�㣬�����Ħ�������ڻ���Ħ��������
��ͼ��ʾ������Ϊm����ΪL���Ҷ���һ��ֱ��֧�ܵľ��ȳ�ľ��ƽ���������ϣ������֮һ�������ھ�ֹ״̬���ֱַ����ᵯ�ɳ�A��Bͨ��ϸ���볤ľ����������֪��ľ����ˮƽ�����Ķ�Ħ��������=0.6����=60�㣬�����Ħ�������ڻ���Ħ���������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 һ���������ӳ�ˮƽ״̬��MΪ�����е㣬����P��Qͬʱ��ʼ������С��ʱ�������IJ�����ͼ������������ϸ����������������ж���ȷ�ģ�������
һ���������ӳ�ˮƽ״̬��MΪ�����е㣬����P��Qͬʱ��ʼ������С��ʱ�������IJ�����ͼ������������ϸ����������������ж���ȷ�ģ�������| A�� | ��ԴQ�����IJ����ȵ����е�M | B�� | ��ԴP�������������µ� | ||
| C�� | �е�M����ʼ���Ǽ�ǿ�� | D�� | M���λ�ƴ�С��ijʱ�̿���Ϊ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 �ҹ�δ��������������أ��������������Ͻ���ռ�վ����ͼ��ʾ���رշ������ĺ���ɻ���������������������Բ�������������������Բ����Ľ��µ�B����ռ�վC�Խӣ���֪�ռ�վ������Բ����İ뾶Ϊr������ΪT����������ΪG������İ뾶ΪR������˵������ȷ���ǣ�������
�ҹ�δ��������������أ��������������Ͻ���ռ�վ����ͼ��ʾ���رշ������ĺ���ɻ���������������������Բ�������������������Բ����Ľ��µ�B����ռ�վC�Խӣ���֪�ռ�վ������Բ����İ뾶Ϊr������ΪT����������ΪG������İ뾶ΪR������˵������ȷ���ǣ�������| A�� | ���������ΪM=$\frac{4{��}^{2}{r}^{3}}{G{T}^{2}}$ | |
| B�� | ����ĵ�һ�����ٶ�Ϊv=$\frac{2��r}{T}$ | |
| C�� | ����ɻ���ͼʾAλ�÷���B�Ĺ����У����ٶ���� | |
| D�� | Ҫʹ����ɻ��Ϳռ�վ�Խӳɹ����ɻ��ڽӽ�B��ʱ������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com