
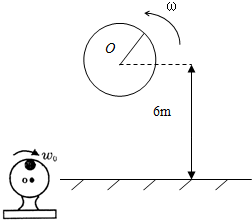
 如图所示,另一种电动打夯机的示意图,在总质量为M的电动机的飞轮上,在距离转轴O为L处固定有一质量为m的重小球.如果飞轮匀速转动,
如图所示,另一种电动打夯机的示意图,在总质量为M的电动机的飞轮上,在距离转轴O为L处固定有一质量为m的重小球.如果飞轮匀速转动,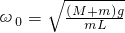 …④
…④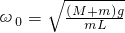 ;
;

 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中物理 来源: 题型:
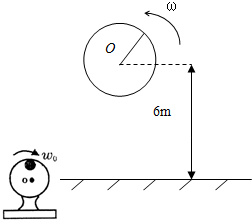 如图所示,另一种电动打夯机的示意图,在总质量为M的电动机的飞轮上,在距离转轴O为L处固定有一质量为m的小球.如果飞轮匀速转动,
如图所示,另一种电动打夯机的示意图,在总质量为M的电动机的飞轮上,在距离转轴O为L处固定有一质量为m的小球.如果飞轮匀速转动,查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
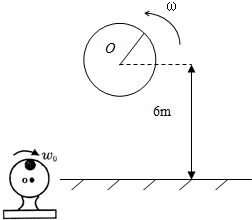
查看答案和解析>>
科目:高中物理 来源:《第6章 曲线运动》2011年单元测试卷(独山子中学)(解析版) 题型:解答题
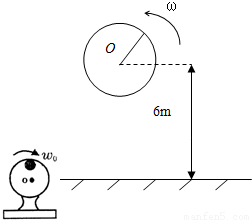
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com