
 如图所示,是游乐场翻滚过山车示意图,斜面轨道AC,弯曲、水平轨道CDE和半径R=7.5m的竖直圆形轨道平滑连接.质量m=100kg的实验小车,从距水平面H=20m高处的A点静止释放,通过最低点C后沿圆形轨道运动一周后进入弯曲、水平轨道CDE.重力加速度g=10m/s2,AC与水平面的倾角θ=37°,小车与AC的摩擦因数μ=0.3,其余不计摩擦和阻力.(sin37°=0.6,cos37°=0.8)求:
如图所示,是游乐场翻滚过山车示意图,斜面轨道AC,弯曲、水平轨道CDE和半径R=7.5m的竖直圆形轨道平滑连接.质量m=100kg的实验小车,从距水平面H=20m高处的A点静止释放,通过最低点C后沿圆形轨道运动一周后进入弯曲、水平轨道CDE.重力加速度g=10m/s2,AC与水平面的倾角θ=37°,小车与AC的摩擦因数μ=0.3,其余不计摩擦和阻力.(sin37°=0.6,cos37°=0.8)求:| H |
| sin37° |
| 1 |
| 2 |
| ||
| R |
| ||
| R |
| gR |
| 10×7.5 |
| 3 |
| H |
| sin37° |
| H′ |
| sin37° |
| 1 |
| 2 |
| h |
| sin37° |


科目:高中物理 来源: 题型:
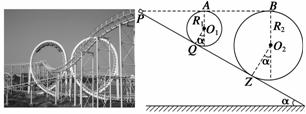
如图所示,左图是游乐场中过山车的实物图片,右图是过山车的原理图.在原理图中半径分别为R1=2.0 m和R2=8.0 m的两个光滑圆形轨道,固定在倾角为α=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使小车(视作质点)从P点以一定的初速度沿斜面向下运动.已知斜轨道面与小车间的动摩擦因数为μ=![]() ,g=10 m/s2,sin37°=0.6,cos37°=0.8.问:
,g=10 m/s2,sin37°=0.6,cos37°=0.8.问:

(1)若小车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为多大?
(2)若小车在P点的初速度为10 m/s,则小车能否安全通过两个圆形轨道?
查看答案和解析>>
科目:高中物理 来源: 题型:
(18分)如图所示,左图是游乐场中过山车的实物图片,右图是过山车的原理图.在原理图中半径分别为R1=2.0 m和R2=8.0 m的两个光滑圆形轨道,固定在倾角为α=37°斜轨道面上的Q、Z两点,且两圆形轨道的最高点A、B均与P点平齐,圆形轨道与斜轨道之间圆滑连接.现使小车(视作质点)从P点以一定的初速度沿斜面向下运动.已知斜轨道面与小车间的动摩擦因数为μ=![]() ,g=10 m/s2,sin37°=0.6,cos37°=0.8.问:
,g=10 m/s2,sin37°=0.6,cos37°=0.8.问:
(1)若小车恰好能通过第一个圆形轨道的最高点A处,则其在P点的初速度应为多大?
(2)若小车在P点的初速度为10 m/s,则小车能否安全通过两个圆形轨道?
查看答案和解析>>
科目:高中物理 来源: 题型:
如图10所示,是游乐场翻滚过山车示意图,斜面轨道AC、弯曲、水平轨道CDE和半径R=7.5m的竖直圆形轨道平滑连接。质量m=100kg的小车,从距水平面H=20m高处的A点静止释放,通过最低点C后沿圆形轨道运动一周后进入弯曲、水平轨道CDE。重力加速度g=10m/s2,不计摩擦力和阻力。求:
(1)若小车从A点静止释放到达圆形轨道最低点C时的速度大小;
(2)小车在圆形轨道最高点B时轨道对小车的作用力;
(3)为使小车通过圆形轨道的B点,相对于C点的水平面小车下落高度的范围。

查看答案和解析>>
科目:高中物理 来源: 题型:
(2013北京市海淀区质检)如图10所示,是游乐场翻滚过山车示意图,斜面轨道AC、弯曲、水平轨道CDE和半径R=7.5m的竖直圆形轨道平滑连接。质量m=100kg的小车,从距水平面H=20m高处的A点静止释放,通过最低点C后沿圆形轨道运动一周后进入弯曲、水平轨道CDE。重力加速度g=10m/s2,不计摩擦力和阻力。求:
(1)若小车从A点静止释放到达圆形轨道最低点C时的速度大小;
(2)小车在圆形轨道最高点B时轨道对小车的作用力;
(3)为使小车通过圆形轨道的B点,相对于C点的水平面小车下落高度的范围。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com