在某公园建有一山坡滑草运动项目,该山坡可看成倾角θ=37°的斜面,一名游客连同滑草装置总质量m=80kg,他从静止开始从顶端匀加速下滑,装置与草之间的动摩擦因数为μ=0.5,山坡长x=64m.(不计空气阻力,取g=10m/s2,)问:
(1)游客连同滑草装置在下滑过程中加速度为多大;
(2)滑到底端时的速度及所用时间.

解:
(1)设游客连同滑草装置在下滑过程中加速度为a,对游客连同滑草装置受力分析如图所示.
由牛顿第二定律得mgsin37°-F
f=ma ①
F
N=mgcos37° ②
又F
f=μF
N ③
联立①②③式解得a=2m/s
2.
(2)设游客连同滑草装置滑到底端时的速度为v,所用时间为t.
由运动学公式可得v
2=2ax,v=at,
解得v=16m/s,t=8s.
答:(1)游客连同滑草装置在下滑过程中加速度为2m/s
2;
(2)滑到底端时的速度为v=16m/s,所用时间为t=8s.
分析:(1)游客连同滑草装置在下滑过程中受到重力、支持力和滑动摩擦力,根据牛顿第二定律和摩擦力公式求解加速度大小.
(2)由运动学位移与速度关系公式和位移公式求出滑到底端时的速度及所用时间.
点评:本题是简单的动力学问题,考查综合应用牛顿定律和运动学公式的能力.对于第(2)问也可以根据动能定理这样列式求解速度v:(mgsin37°-μmgcos37°)x=
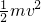
.

 解:
解: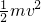 .
. 
