
分析 快中子与碳原子发生弹性碰撞,动量守恒和机械能守恒,根据两大守恒列式求解出经一次碰撞后中子的能量为E1=($\frac{11}{13}$)2E0,根据碰撞过程的规律得到碰撞2次、3次、4次…n次后中子的能量,即可求出碰撞次数
解答 解:设中子和碳核的质量分别为m和M,碰撞前中子的速度为v0,碰撞后中子和碳核的速度分别为v和v′,
因为碰撞是弹性碰撞,所以在碰撞前后,动量和机械能均守恒,又因v0、v和v′沿同一直线,
以碰撞前中子的速度方向为正方向,由动量守恒定律得:mv0=mv+Mv′
由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv2+$\frac{1}{2}$Mv′2
解得:v=$\frac{m-M}{m+M}$v0 已知:M=12m,
解得:v=-$\frac{11}{13}$v0,负号表示v的方向与v0方向相反,即与碳核碰撞后中子被反弹.
因此,经过一次碰撞后中子的能量为:E1=$\frac{1}{2}$mv2=($\frac{11}{13}$)2E0,
经过2,3,…,n次碰撞后,中子的能量依次为E2,E3,E4,…,En,有
E2=($\frac{11}{13}$)2E1=($\frac{11}{13}$)2E0
E3=($\frac{11}{16}$)6E0
…
En=($\frac{{E}_{1}}{{E}_{0}}$)nE0=($\frac{11}{13}$)2nE0
因此:n=$\frac{1}{2}$$\frac{lg\frac{{E}_{n}}{{E}_{0}}}{lg\frac{11}{13}}$,$\frac{{E}_{n}}{{E}_{0}}$=$\frac{0.025}{1.75×1{0}^{6}}$=$\frac{1}{7}$×10-7,n=$\frac{lg(\frac{1}{7}×1{0}^{-7})}{2lg(\frac{11}{13})}$≈54
故初能量E0=1.75MeV的快中子经过近54次碰撞后,才成为能量为0.025eV的热中子.
答:一个动能为E0=1.75MeV的快中子需要与静止的碳原子碰撞54次,才能减速成为0.025eV的热中子.
点评 本题考查了动量守恒定律的应用,解决本题的关键知道弹性碰撞的过程中动量守恒,能量也守恒,列式后找出规律进行求解.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:解答题
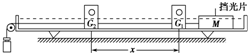 为了探究加速度与力的关系,使用如实图所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,它们与数字计时器相连,当滑行器通过G1、G2光电门时,光束被遮挡的时间△t1、△t2都可以被测量并记录,滑行器连同上面固定的一条形挡光片的总质量为M,挡光片宽度为d,光电门间距离为X,牵引砝码的质量为m.回答下列问题:
为了探究加速度与力的关系,使用如实图所示的气垫导轨装置进行实验.其中G1、G2为两个光电门,它们与数字计时器相连,当滑行器通过G1、G2光电门时,光束被遮挡的时间△t1、△t2都可以被测量并记录,滑行器连同上面固定的一条形挡光片的总质量为M,挡光片宽度为d,光电门间距离为X,牵引砝码的质量为m.回答下列问题:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 我校的田径运动会将在本月13日开始进行,4×100m接力跑是最具有看点的比赛.而接棒是比赛的重中之重.甲、乙两个同学在直跑道上练习4×100m接力跑,如图所示,他们在奔跑时有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀变速运动.现在甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑达到最大速度的80%,则下述正确的有( )
我校的田径运动会将在本月13日开始进行,4×100m接力跑是最具有看点的比赛.而接棒是比赛的重中之重.甲、乙两个同学在直跑道上练习4×100m接力跑,如图所示,他们在奔跑时有相同的最大速度.乙从静止开始全力奔跑需跑出25m才能达到最大速度,这一过程可看作匀变速运动.现在甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑达到最大速度的80%,则下述正确的有( )| A. | 乙接棒时在接力区需奔出8m的距离 | |
| B. | 乙接棒时在接力区需奔出16m的距离 | |
| C. | 乙应在距离甲16m时起跑 | |
| D. | 乙应在距离甲24m时起跑 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
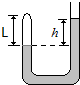 如图所示粗细均匀的U形管竖直放置,左端封闭,右端大气,大气压为p0,管内注入水银,两边水银面的高度差为h,左管空气柱的长度为L.
如图所示粗细均匀的U形管竖直放置,左端封闭,右端大气,大气压为p0,管内注入水银,两边水银面的高度差为h,左管空气柱的长度为L.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 光电管的阴极材料是钠.使钠产生光电效应的极限波长λ0=5000A,若光电管阴极和阳极间加电压2.1V,用λ=3000A的紫外张照射,饱和电流是0.56×10-6A,试谋算:
光电管的阴极材料是钠.使钠产生光电效应的极限波长λ0=5000A,若光电管阴极和阳极间加电压2.1V,用λ=3000A的紫外张照射,饱和电流是0.56×10-6A,试谋算:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
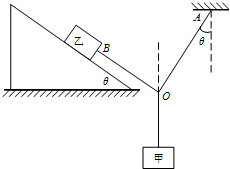 如图所示,重为25N的物体甲通过三段绳悬挂,三段轻绳的结点为O,轻绳OB平行于倾角为37°的斜面,且B端与放置在斜面上的重为100N的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙都处于静止状态,求:
如图所示,重为25N的物体甲通过三段绳悬挂,三段轻绳的结点为O,轻绳OB平行于倾角为37°的斜面,且B端与放置在斜面上的重为100N的物体乙相连,轻绳OA与竖直方向的夹角θ=37°,物体甲、乙都处于静止状态,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 小灯泡通电后,其电流I随所加电压U变化的图线如图所示,P为图线上一点,PN为图线的切线,则下列说法正确的是( )
小灯泡通电后,其电流I随所加电压U变化的图线如图所示,P为图线上一点,PN为图线的切线,则下列说法正确的是( )| A. | 随着所加电压的增大,小灯泡的电阻增大 | |
| B. | 对应P点,小灯泡的电阻为R=$\frac{{U}_{1}}{{I}_{2}-{I}_{1}}$ | |
| C. | 对应P点,小灯泡的电阻为R=$\frac{{U}_{1}}{{I}_{2}}$ | |
| D. | 对应P点,小灯泡的功率为P=U1I2 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 当分子间距离为r0时,它们之间既没有斥力也没有引力 | |
| B. | 分子间的引力和斥力都随分子间距离的增大而减小 | |
| C. | 温度计读出的示数是它自身这个系统的温度,若它与被测系统热平衡时,这一示数也是被测系统的温度 | |
| D. | 物体的机械能损失时,内能却可以增加 | |
| E. | 布朗运动就是液体分子的热运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
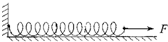 在光滑水平面上有一根轻质弹簧,将弹簧一端固定,另一端施以水平拉力F时,弹簧伸长量为x1,如图所示;当水平拉力2F时,弹簧伸长量为x2,弹簧始终处在弹性限度内,则( )
在光滑水平面上有一根轻质弹簧,将弹簧一端固定,另一端施以水平拉力F时,弹簧伸长量为x1,如图所示;当水平拉力2F时,弹簧伸长量为x2,弹簧始终处在弹性限度内,则( )| A. | x2=x1 | B. | x2=2x1 | C. | x2=3x1 | D. | x2=4x1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com