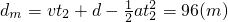Question

一列货车以v=8m/s的速度沿平直的公路匀速行驶，在它的后面d=80m处有一辆汽车从静止开始启动匀加速追及货车，加速度大小为a=2m/s²，当汽车速度增加到最大速度v_m=20m/s后，停止加速改为以最大速度匀速追及．试求：
（1）汽车启动后经多长时间速度达到最大值；
（2）汽车启动后经多长时间汽车追上货车；
（3）追及过程中两车间的最大距离是多少．

Answer 1

解：（1）汽车启动后，匀加速过程中 at₁=v_m
解得 t₁=10（s）
即经过10s汽车达到最大速度
（2）设汽车经过t时间追上货车，t₁为汽车加速到最大速度的时间．
则应有：
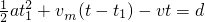
解得，t=15（s）
（3）设经历时间t₂两车速度相等时，此时两车之间距离最大，有
at₂=v
所以 t₂=4（s）
两车间距最大距离为：
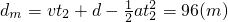
答：（1）汽车经过10s汽车达到最大速度．
（2）汽车启动后经15s时间汽车追上货车；
（3）追及过程中两车间的最大距离是96m．
分析：（1）根据匀变速直线运动的速度时间公式求出汽车达到最大速度经历的时间．
（2）汽车追及货车的过程经历了匀加速直线运动和匀速直线运动，抓住位移关系，根据运动学公式求出追及的时间．
（3）两车速度相等前，货车的速度大于汽车的速度，两车的距离越来越大，速度相等后，货车的速度小于汽车的速度，两车的距离越来越小，知当速度相等时，两车间距最大．根据速度时间公式和位移时间公式求出相距的最大距离．
点评：本题是追及问题，抓住位移关系，运用运动学公式灵活求解．