
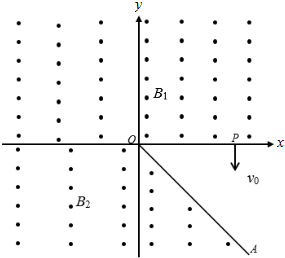
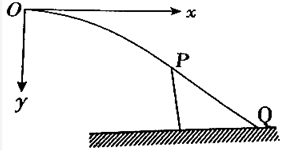
 ��ͼ��ʾ����xOyƽ���ڣ���x���Ϸ��дŸ�Ӧǿ��ΪB1��ֱƽ��������ǿ�ų�����x���·�����xOA��������������ƽ��x�����ǿ�糡��ͼ��δ�������⣬�����������дŻ�Ӧǿ��ΪB2��ֱƽ���������ǿ�ų���B1��B2��Сĩ֪����B1=$\frac{4}{3}$B2��һ�����ٶ�Ϊv0�Ĵ���������ӣ���x���ϵ�P�㴹ֱx�����xOA�������ǿ�糡�У����Ӿ���0A��ʱ���ٶȷ����Ǵ�ֱOA�ߵģ��ٴξ���x����������ϵ�Q��ʱ��Q��δ�������ٶȷ���Ҳ����x�ᴹֱ����������û�д�OA�߽���糡����֪����XOA=45�㣬P��������ǣ�L��0�����������ӵ�����Ϊm�������Ϊq�����ƴ�����������������
��ͼ��ʾ����xOyƽ���ڣ���x���Ϸ��дŸ�Ӧǿ��ΪB1��ֱƽ��������ǿ�ų�����x���·�����xOA��������������ƽ��x�����ǿ�糡��ͼ��δ�������⣬�����������дŻ�Ӧǿ��ΪB2��ֱƽ���������ǿ�ų���B1��B2��Сĩ֪����B1=$\frac{4}{3}$B2��һ�����ٶ�Ϊv0�Ĵ���������ӣ���x���ϵ�P�㴹ֱx�����xOA�������ǿ�糡�У����Ӿ���0A��ʱ���ٶȷ����Ǵ�ֱOA�ߵģ��ٴξ���x����������ϵ�Q��ʱ��Q��δ�������ٶȷ���Ҳ����x�ᴹֱ����������û�д�OA�߽���糡����֪����XOA=45�㣬P��������ǣ�L��0�����������ӵ�����Ϊm�������Ϊq�����ƴ��������������������� ��1��������������ǿ�糡������ƽ���˶����������ܵĵ糡������ȷ���糡ǿ�ȵķ�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ�����ǿE��
��2�����ݼ��ι�ϵ�����������ǿ�ų�${B}_{2}^{\;}$�еİ뾶���������������ṩ���������${B}_{2}^{\;}$����${B}_{1}^{\;}$��${B}_{2}^{\;}$�Ĺ�ϵ���${B}_{1}^{\;}$��
��3���ֱ����������ƽ��ʱ�������ǿ�ų�${B}_{1}^{\;}$��${B}_{2}^{\;}$�е�����Բ���˶�����ʱ��֮�ͣ���������������Ӵ�P���˶���Q���ʱ�䣻
��4�����ݼ��ι�ϵ���P��Q�����ľ��룻
��� 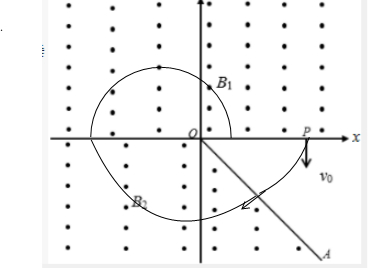 �⣺��1��������������ǿ�糡������ƽ���˶�����֪���������ܵ��糡��ƽ��x�ᣬ������x�Ḻ�������ڴ������Ӵ����磬���Ե糡ǿ�ȷ���ƽ��x�ᣬ��x�Ḻ����
�⣺��1��������������ǿ�糡������ƽ���˶�����֪���������ܵ��糡��ƽ��x�ᣬ������x�Ḻ�������ڴ������Ӵ����磬���Ե糡ǿ�ȷ���ƽ��x�ᣬ��x�Ḻ����
��ţ�ٵڶ����ɵã��������ӵļ��ٶ�$a=\frac{qE}{m}$
������ƽ���˶����ɿɵã�
x�᷽��$x=\frac{1}{2}a{t}_{1}^{2}$��${v}_{x}^{\;}=a{t}_{1}^{\;}$
y�᷽��$y={v}_{0}^{\;}{t}_{1}^{\;}$
$tan45��=\frac{{v}_{y}^{\;}}{{v}_{0}^{\;}}$
�ɼ��ι�ϵ�ɵã�x+y=L
���Ͻ�ã�$E=\frac{3m{v}_{0}^{2}}{2qL}$��${t}_{1}^{\;}=\frac{2L}{3{v}_{0}^{\;}}$��$y=\frac{2L}{3}$
��2�����������ڴų����˶����ٶ�$v=\sqrt{2}{v}_{0}^{\;}$
���Ӿ���OA��ʱ���ٶȷ����Ǵ�ֱOA�ߵģ��ٴξ���x����������ϵ�Q��ʱ���ٶ�Ҳ����x�ᴹֱ��˵���������Ӿ���x�Ḻ����ʱ��Ҳ��x�ᴹֱ�����Դ�����������ǿ�ų�${B}_{2}^{\;}$��������Բ���˶���Բ�ľ���ԭ��O��������������ǿ�ų�${B}_{2}^{\;}$����Բ���˶��İ뾶${r}_{2}^{\;}=\sqrt{2}y=\frac{2\sqrt{2}}{3}L$
������Բ���˶��������������������ṩ
$qv{B}_{2}^{\;}=m\frac{{v}_{\;}^{2}}{{r}_{2}^{\;}}$����ã�${B}_{2}^{\;}=\frac{mv}{q{r}_{2}^{\;}}=\frac{3m{v}_{0}^{\;}}{2qL}$������${B}_{1}^{\;}=\frac{4}{3}{B}_{2}^{\;}=\frac{2m{v}_{0}^{\;}}{qL}$
��������ǿ�ų�${B}_{2}^{\;}$����Բ���˶���ʱ��${t}_{2}^{\;}=\frac{s}{v}=\frac{\frac{3}{4}��{r}_{2}^{\;}}{v}=\frac{��L}{2{v}_{0}^{\;}}$
��3����������ǿ�ų�${B}_{1}^{\;}$����Բ���˶��������������������ṩ
$qv{B}_{1}^{\;}=m\frac{{v}_{\;}^{2}}{{r}_{1}^{\;}}$����ã�${r}_{1}^{\;}=\frac{mv}{q{B}_{1}^{\;}}=\frac{\sqrt{2}}{2}L$
��������ǿ�ų�${B}_{1}^{\;}$����Բ���˶���ʱ��${t}_{3}^{\;}=\frac{s��}{v}=\frac{��{r}_{1}^{\;}}{v}=\frac{��L}{2{v}_{0}^{\;}}$
���Դ������Ӵ�P���˶���Q���ʱ��$t={t}_{1}^{\;}+{t}_{2}^{\;}+{t}_{3}^{\;}=\frac{��2+3�У�L}{3{v}_{0}^{\;}}$
��4��P��Q�����ľ���$��x=L+{r}_{2}^{\;}-2{r}_{1}^{\;}=\frac{3-\sqrt{2}}{3}L$
�𣺣�1����ǿ�糡�ĵ糡ǿ�ȵķ�����x�Ḻ����СΪ$\frac{3m{v}_{0}^{2}}{2qL}$
��2����ǿ�ų��ĴŸ�Ӧǿ��B1�Ĵ�С$\frac{2m{v}_{0}^{\;}}{2qL}$
��3���������Ӵ�P���˶���Q���ʱ��$\frac{��2+3�У�L}{3{v}_{0}^{\;}}$
��4��P��Q�����ľ���$\frac{3-\sqrt{2}}{3}L$
���� �����������������Բ���˶�����ƽ���˶��У���ţ�ٵڶ��������˶�ѧ��ʽ������ϼ��ι�ϵ�������������˶���ǿ���˶��ķֽ⣬��ͻ��ȷ���˶��켣ͼ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��ˮƽϸ������һϸ��A����A����B����һ�����������������ֱ�ΪmA��mB������B���ܵ�ˮƽ����F�����ã�A����B��һ�����������˶���������ֱ����ļн�Ϊ�ȣ�������˵����ȷ���ǣ�������
��ͼ��ʾ��ˮƽϸ������һϸ��A����A����B����һ�����������������ֱ�ΪmA��mB������B���ܵ�ˮƽ����F�����ã�A����B��һ�����������˶���������ֱ����ļн�Ϊ�ȣ�������˵����ȷ���ǣ�������| A�� | B���ܵ��ĺ���FСΪmAg+tan�� | |
| B�� | ����B�������Ϊ$\frac{{m}_{B}g}{sin��}$ | |
| C�� | �˶�A���ĵ���Ϊ��mA+mB��g | |
| D�� | A����˵Ķ�Ħ������Ϊ$\frac{{m}_{B}}{{m}_{A}+{m}_{B}}$tan�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
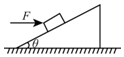 ��ͼ��ʾ��б����Ǧȣ�б�����һ����Ϊm�����壬������б���Ļ���Ħ��ϵ���̣�����һˮƽ��Fʹ���������˶���������ļ��ٶȣ�
��ͼ��ʾ��б����Ǧȣ�б�����һ����Ϊm�����壬������б���Ļ���Ħ��ϵ���̣�����һˮƽ��Fʹ���������˶���������ļ��ٶȣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
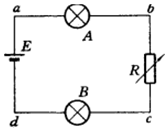 ��ͼ��ʾ��·�е���A��B������������·��ֻ��һ���Ͽ���������ѹ�����Uab=0��Uac=0��Ubd=3V��Ucd=3V����ɷ�������������
��ͼ��ʾ��·�е���A��B������������·��ֻ��һ���Ͽ���������ѹ�����Uab=0��Uac=0��Ubd=3V��Ucd=3V����ɷ�������������| A�� | B�ƶϿ� | B�� | A�ƶϿ� | C�� | ��Դ�Ͽ� | D�� | R�Ͽ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
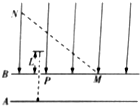 ��ͼ��ʾ��ƽ�н�����A��B����ڼ��ٵ�ѹ��һ������������������ɵ����Ӵ�A�帽���ɾ�ֹ��ʼ�����٣�ǡ�ô�B��С��P�ɳ���B���Ϸ��ֲ��г�ǿΪE����ǿ�糡������ǿ������ֱ����ʱ�����Ӵ�С��P����糡�����ڵ糡�����������߶�ΪL���ռ�������M��N������B���45��ǣ�
��ͼ��ʾ��ƽ�н�����A��B����ڼ��ٵ�ѹ��һ������������������ɵ����Ӵ�A�帽���ɾ�ֹ��ʼ�����٣�ǡ�ô�B��С��P�ɳ���B���Ϸ��ֲ��г�ǿΪE����ǿ�糡������ǿ������ֱ����ʱ�����Ӵ�С��P����糡�����ڵ糡�����������߶�ΪL���ռ�������M��N������B���45��ǣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��С����3m/s���ٶ�ˮƽ�׳���������ٶ�Ϊ5m/s����vx��vy�ֱ��ʾˮƽ����ֱ���ٶȣ���ay��ʾ��ֱ�ּ��ٶȣ�ȡg=10m/s2����ͼ����ȷ���ǣ�������
��С����3m/s���ٶ�ˮƽ�׳���������ٶ�Ϊ5m/s����vx��vy�ֱ��ʾˮƽ����ֱ���ٶȣ���ay��ʾ��ֱ�ּ��ٶȣ�ȡg=10m/s2����ͼ����ȷ���ǣ�������| A�� | 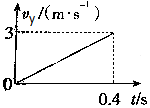 | B�� | 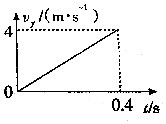 | ||
| C�� | 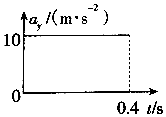 | D�� | 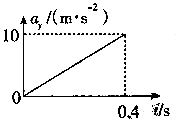 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com