
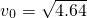 m/s沿虚线向圆心O点滑出.为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好.按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒.已知冰壶石与冰面间动摩擦因数μ1=0.008,甲方运动员通过刷冰可使动摩擦因数μ2减小到0.002,乙方运动员通过刷冰可使动摩擦因数μ3减小到0.0025.两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的
m/s沿虚线向圆心O点滑出.为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好.按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒.已知冰壶石与冰面间动摩擦因数μ1=0.008,甲方运动员通过刷冰可使动摩擦因数μ2减小到0.002,乙方运动员通过刷冰可使动摩擦因数μ3减小到0.0025.两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的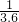 ,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2.比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石.等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分.求:
,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2.比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石.等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分.求: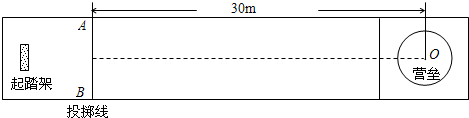




 m/s
m/s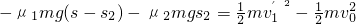


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中物理 来源: 题型:
| 4.64 |
| 1 |
| 3.6 |

查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
| 4.64 |
| 1 |
| 3.6 |
查看答案和解析>>
科目:高中物理 来源:北京模拟题 题型:计算题
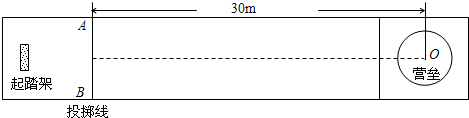
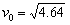 m/s沿虚线向圆心O点滑出。为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好。按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒。已知冰壶石与冰面间动摩擦因数
m/s沿虚线向圆心O点滑出。为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好。按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒。已知冰壶石与冰面间动摩擦因数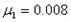 ,甲方运动员通过刷冰可使动摩擦因数
,甲方运动员通过刷冰可使动摩擦因数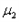 减小到0.002,乙方运动员通过刷冰可使动摩擦因数
减小到0.002,乙方运动员通过刷冰可使动摩擦因数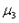 减小到0.0025。两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的
减小到0.0025。两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的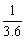 ,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2。比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石。等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分。求:
,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2。比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石。等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分。求: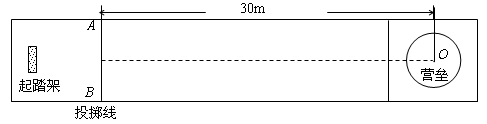
查看答案和解析>>
科目:高中物理 来源:2012年北京市通州区高考物理二模试卷(解析版) 题型:解答题
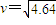 m/s沿虚线向圆心O点滑出.为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好.按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒.已知冰壶石与冰面间动摩擦因数μ1=0.008,甲方运动员通过刷冰可使动摩擦因数μ2减小到0.002,乙方运动员通过刷冰可使动摩擦因数μ3减小到0.0025.两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的
m/s沿虚线向圆心O点滑出.为保证比赛胜利,使冰壶石C能滑到圆心O点,将对方已停在O点的冰壶石D碰走,同时保证甲方冰壶石C能留在营垒内,且离圆心越近越好.按比赛规则,甲方运动员可在场地内任意位置刷冰,减小动摩擦因数,使冰壶石C以适当的速度碰走冰壶石D,乙方运动员可在两冰壶石相碰后越过D点时刷冰,减小动摩擦因数使冰壶石C滑出营垒.已知冰壶石与冰面间动摩擦因数μ1=0.008,甲方运动员通过刷冰可使动摩擦因数μ2减小到0.002,乙方运动员通过刷冰可使动摩擦因数μ3减小到0.0025.两冰壶石发生正碰,碰撞过程中系统能量损失为冰壶石C碰撞前动能的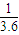 ,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2.比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石.等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分.求:
,碰撞前后两冰壶石始终在同一直线上运动,g取10m/s2.比赛中两方依次投冰壶石,每队有4个人,每个人2个冰壶石.等到双方将冰壶石全部投完之后,一局便结束了,此时开始计算得分.求: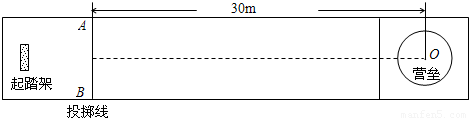
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com