
阅读以下有关加速器的文章完成文中问题(问题以加粗字体标记)。
相关知识背景:
电子伏特,符号为eV,是能量的单位。代表一个电子经过1伏特的电势差加速后所获得的动能。在微观领域,一般使用电子伏特作为能量单位。电子伏特与SI制的能量单位焦耳(J)的换算关系是单位换算:1eV=1.6×10-19J 1MeV=1×106 eV
a粒子即为氦原子核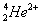
科学家在研究原子核的结构时,采用了高速运动的亚原子粒子去轰击原子核.早在1906年,卢瑟福就利用放射性物质释放的高速α粒子来轰击物质.1919年他成功地从氮原子核中打出了质子,使氮原子核变成氧原子核.然而使用天然产生的α粒子作为轰击物,有很大的局限性.带正电的α粒子与带正电的原子核相互排斥,要消耗很大的能量;而天然产生的带电粒子的能量是有限的.为了得到更高能量的带电粒子,物理学家们开始尝试设计一种产生高能量带电粒子的实验设备——加速器.我们知道电场可以使带电粒子加速,增加带电粒子的能量。
(1)如图所示,这就是早期的加速器的原理。若设该加速器两板间电压为1000V,两板间距为20厘米,求一初速度可忽略不计的α粒子通过该加速器所获得的能量?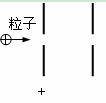
这种加速器可以通过增加电极间的电压来提高粒子加速的能量,但这种加速器的发展受到高压绝缘的限制。(电压太大,电介质会被击穿)。
因此,人们就想利用较低的电压,采用多级加速使粒子加速到高能量,如图甲所示。N个长度逐个增大的金属圆筒和一个靶,它们沿轴线排列成一串,如图所示(图中只画出了六个圆筒,作为示意)。各筒和靶相间地连接到如图乙所示周期为T、电压值为U0的高频方波电源的两端。整个装置放在高真空容器中,圆筒的两底面中心开有小孔。带电粒子沿轴线射入圆筒,并将在圆筒间及圆筒与靶间的缝隙处受到电场力的作用而加速(设圆筒内部没有电场)。缝隙的宽度很小,粒子穿过缝隙的时间可以不计。
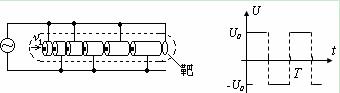
(2)为使初动能为2U0e、质量为mα的α粒子打到靶时获得最大能量,各个圆筒的长度应满足什么条件?
(3)在满足第(2)问条件的前提下,若用该加速器加速一初动能为2U0e的α粒子,求α粒子进入第k个圆筒前与进入第n个圆筒前的速率之比vk:vn。(k和n均为自然数)
(4)若该加速器的电压U0=1×105V,T=0.002s用该加速器加速一初动能2×105eV的α粒子,为使粒子获得40MeV以上的动能,则该加速器的长度至少为多大?(可以用数列形式表示)α粒子质量为mα≈3600MeV/c²(c指光速)
通过刚才的计算我们可以看到,要想达到越来越高的能量,就必须使设备的长度增加到数十甚至数百英里的长度,从而因为经济效益的原因变的不实用。
1931年,加利福尼亚大学的欧内斯特·O·劳伦斯(Ernest O.Lawrence)提出了一个卓越的思想,通过磁场的作用迫使粒子沿着磁极之间作螺旋线运动,把电极像卷尺那样卷起来,这样就可以在有限的场地装设比原来长许多倍的电极,他把这种设备叫作“回旋加速器”。
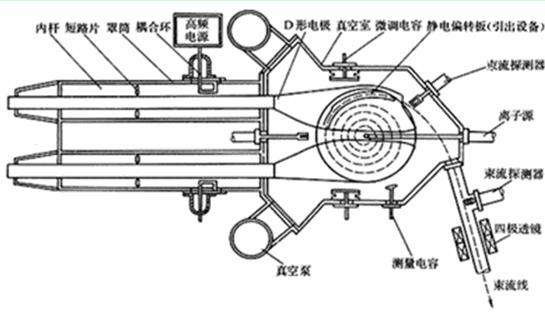
回旋加速器主要由圆柱形磁极、D形盒、高频交变电源、粒子源和引出装置组成,如图所示.其中D形盒装在真空室中,是回旋加速器的核心部件,整个真空室放在磁极之间,磁场方向垂直于D形盒,两个D形盒之间留一个窄缝,分别与高频电源的两极相连.当粒子经过D形盒之间的窄缝,得到高频电源的加速,在D形盒之间,由于屏蔽作用,盒内只有磁场分布,这样带电粒子在D形盒内沿螺线轨道运动,达到预期的速率后,用引出装置引出。
如图所示:若D形盒的半径为R,离子源放出质量为m、带电量为q的正离子,磁感应强度大小为B,求:
(5)加在D形盒间的高频电源的频率。(用字母表示)
(6)从静电偏转板(如图所示)出去的离子所具有的能量。(用字母表示)
(7)若被回旋加速器加速的粒子为初速度可忽略不计的α粒子,若:
α粒子质量为mα≈3600MeV/c²(c指光速), D形盒中的磁感应强度为1T,为使粒子获得40MeV以上的动能,则D形盒的半径R至少为多大?
两相比较,我们发现加速到相同的动能,劳伦斯的回旋加速器的占地面积远小于多级加速器,所以,回旋加速器的出现,使科学家们在实验室中获得高能粒子的愿望得以实现。
40年代以后,物理学家用劳伦斯创造的加速器发现了许多新型核反应,观察到几百种前所未闻的同位素.在实施制造原子弹的曼哈顿工程时,劳伦斯用他的加速器分离出仅占铀的总量0.7% 的铀235,为发明原子弹立下了汗马功劳。
因为发明回旋加速器,劳伦斯获1939年诺贝尔物理学奖。
带电粒子加速器自1930年前后问世以来,主要是朝更高能量的方向发展,在劳伦斯之后,科学家们设计制造了各种类型的新型加速器,如同步加速器、电子感应加速器,对撞机等。任何一种加速器都经历了发生、发展和加速能力或经济效益受到限制的三个阶段。在第三个阶段中,总会出现新技术或新原理突破困难,从而建造出新类型的加速器,使能量进一步提高,或使建造更高能量加速器在经济上成为可行。
【答案】(1)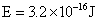 ; (2)
; (2) (3)
(3)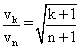 ;
;
(4)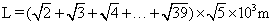 ;
;
(5)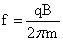 ; (6)
; (6)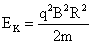 ; (7)
; (7)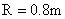 。
。
【解析】
(1)粒子在电场中加速,由动能定理得: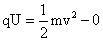 ,
,
则α粒子获得的能量: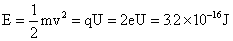 ;
;
(2)粒子在圆筒内做匀速直线运动,当运动的时间等于交流电变化周期的一半时,即为一直处于加速状态,则有: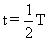 ;
;
由题意,缝隙的宽度很小,粒子穿过缝隙的时间可以不计,所以粒子在圆筒内运动的时间就是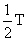
粒子的初动能是2eU0则初速度: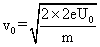
第一个圆筒的长度就是粒子在第一个圆筒内的位移: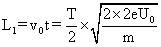
粒子穿过第一个圆筒后的动能: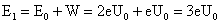 ;
;
粒子穿过第一个圆筒后的速度: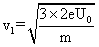
第二个圆筒的长度: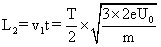
…
粒子穿过第n-1个圆筒后的动能:
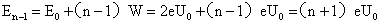 ①
①
粒子穿过第n-1个圆筒后的速度: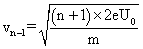 ②
②
第n个圆筒的长度: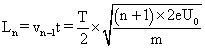 ; ③
; ③
(3)由②可得α粒子进入第k个圆筒前的速度是从第k-1个圆筒中出来的速度,它与进入第n个圆筒前的速率之比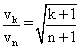 ;
;
(4)设粒子需要穿过n个圆筒,则由①式,穿过n个圆筒后粒子的动能: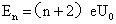
由于粒子的初动能是2eU0则: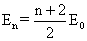
所以: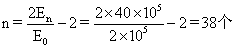 ;
;
圆筒的总长度:
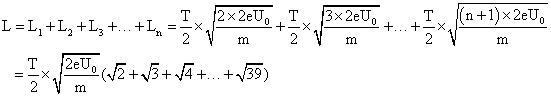
代入数据解得: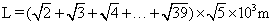 ;
;
(5)使正离子每经过窄缝都被加速,交变电压的频率应等于离子做圆周运动的频率,正离子在磁场中做匀速圆周运动,
洛伦兹力提供向心力,由牛顿第二定律得: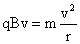 ,
,
得周期: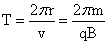 ,频率:
,频率: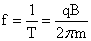 ;
;
(6)由牛顿第二定律得: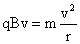 ,解得:
,解得: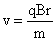 ,
,
当离子从D盒边缘离开时,轨道半径r最大为R,
此时粒子速度最大,最大速度: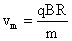 ,
,
离子获得的最大动能: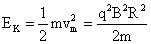 ;
;
(7)粒子的最大动能: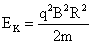 ,
,
则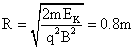 。
。
【考点】带电粒子在匀强电场中的运动;带电粒子在匀强磁场中的运动;牛顿第二定律


科目:高中物理 来源: 题型:
甲、乙两辆卡车质量m甲>m乙,都以相同的额定功率在平直的公路上同向行驶,若卡车所受运动阻力等于车重的K倍(K<1),则两车在行驶过程中
A.有相同的最大速度 B.有相同的最大动量
C.速度相同时牵引力F甲>F乙 D.速度相同时加速度a甲<a乙
查看答案和解析>>
科目:高中物理 来源: 题型:
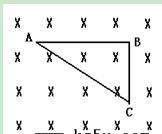
如图,直角三角形闭合线圈ABC处于垂直纸面向里的匀强磁场中,线圈通有顺时针方向电流,则线圈所受磁场力的合力为( )
A.大小为零 B.方向竖直向上
C.方向竖直向下 D.方向垂直纸面向里
查看答案和解析>>
科目:高中物理 来源: 题型:
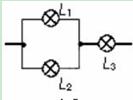
如图所示电路中,三个相同的灯泡额定功率是40 W,在不损坏灯泡的情况下,这三个灯泡消耗的总功率最大不超过 :
A.40 W B.60 W C.80 W D.120 W
查看答案和解析>>
科目:高中物理 来源: 题型:
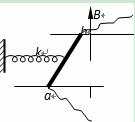
如图所示,长为L的通电直导体棒放在光滑水平绝缘轨道上,劲度系数为k的水平轻弹簧一端固定,另一端拴在棒的中点,且与棒垂直,整个装置处于方向竖直向上、磁感应强度为B的匀强磁场中,弹簧伸长x,棒处于静止状态.则:
A.导体棒中的电流方向从a流向b
B.导体棒中的电流大小为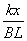
C.若只将磁场方向缓慢顺时针转过一小角度,x变大
D.若只将磁场方向缓慢逆时针转过一小角度,x变大
查看答案和解析>>
科目:高中物理 来源: 题型:
如图所示,质量为m的物体用细绳拴住放在粗糙的水平传送带上,物体距传送带左端的距离为L。当传送带分别以v1、v2的速度逆时针转动(v1<v2),稳定时绳与水平方向的夹角为θ,绳的拉力分别为F1、F2;若剪断细绳时,物体到达左端的时间分别为t1、t2,则下列说法正确的是 ( )
A.F1<F2 B.F1=F2
C.t1一定大于t2 D.t1可能等于t2

查看答案和解析>>
科目:高中物理 来源: 题型:
如图所示,边长为L的正方形PQMN(含边界)区域内有垂直纸面向外的匀强磁场,左侧有水平向右的匀强电场,场强大小为E,质量为m,电量为q的带正电粒子(不计重力)从O点由静止释放,O、P、Q三点在同一水平线上,OP=L,带电粒子恰好从M点离开磁场,求:
(1)磁感应强度B的大小。
(2)粒子从O点到M点经历的时间。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com