
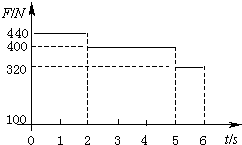
 一质量为m=40kg的小孩在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.
一质量为m=40kg的小孩在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示. a1t2
a1t2 a2(t3-t2)2
a2(t3-t2)2

 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:
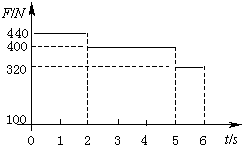 (2006?甘肃)一质量为m=40kg的小孩在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.
(2006?甘肃)一质量为m=40kg的小孩在电梯内的体重计上,电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.查看答案和解析>>
科目:高中物理 来源: 题型:
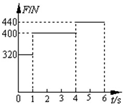 一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始下降,在0到6s内体重计示数F的变化如图所示.
一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始下降,在0到6s内体重计示数F的变化如图所示.查看答案和解析>>
科目:高中物理 来源: 题型:
 一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始上升,在0s到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度是多少?(取重力加速度g=10m/s2.)
一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始上升,在0s到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度是多少?(取重力加速度g=10m/s2.)查看答案和解析>>
科目:高中物理 来源: 题型:
 一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度
一质量为m=40kg的小孩子站在电梯内的体重计上.电梯从t=0时刻由静止开始上升,在0到6s内体重计示数F的变化如图所示.试问:在这段时间内电梯上升的高度查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com