
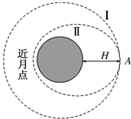
 我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响,万有引力常量为G,求:
我国于2013年12月发射了“嫦娥三号”卫星,该卫星在距月球表面H处的环月轨道Ⅰ上做匀速圆周运动,其运行的周期为T,随后“嫦娥三号”在该轨道上A点采取措施,降至近月点高度为h的椭圆轨道Ⅱ上,如图所示.若以R表示月球的半径,忽略月球自转及地球对卫星的影响,万有引力常量为G,求:分析 (1)根据万有引力提供圆周运动向心力求得中心天体月球的质量;
(2)根据万有引力提供圆周运动向心力求得月球的第一宇宙速度;
(3)根据开普勒第三定律求得在椭圆轨道上的周期.
解答 解:(1)由题意知,在轨道I上卫星运动时万有引力提供圆周运动向心力有:
$G\frac{mM}{(R+H)^{2}}=m(R+H)(\frac{2π}{T})^{2}$
可得月球质量为:M=$\frac{4{π}^{2}(R+H)^{3}}{G{T}^{2}}$
(2)第一宇宙速度是近月卫星的环绕速度,根据万有引力提供圆周运动向心力有:
$G\frac{mM}{{R}^{2}}=m\frac{{v}^{2}}{R}$
可得月球的第一宇宙速度为:$v=\sqrt{\frac{GM}{R}}$=$\frac{2π}{RT}\sqrt{R(R+H)^{3}}$
(3)根据开普勒第三定律:在轨道Ⅰ和轨道Ⅱ上的周期满足:
$\frac{{R}_{I}^{3}}{{T}_{I}^{2}}=\frac{{R}_{II}^{3}}{{T}_{II}^{2}}$
可得卫星在椭圆轨道上运动的周期为:
${T}_{II}=\sqrt{\frac{{R}_{II}^{3}}{{R}_{I}^{3}}}{T}_{I}$=$\sqrt{(\frac{\frac{2R+H+h}{2}}{R+H}})^{3}T$=$\sqrt{\frac{(2R+H+h)^{3}}{8(R+H)^{3}}}T$
答:(1)月球的质量为$\frac{4{π}^{2}(R+H)^{3}}{G{T}^{2}}$;
(2)月球的第一宇宙速度为$\frac{2π}{RT}\sqrt{R(R+H)^{3}}$;
(3)“嫦娥三号”在图中椭圆轨道Ⅱ上的周期为$\sqrt{\frac{(2R+H+h)^{3}}{8(R+H)^{3}}}T$.
点评 万有引力提供圆周运动向心力与万有引力与重力相等,这是万有引力应用的主要解题入手点,掌握万有引力及向心力的不同表达式是正确解题的基础,不难属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
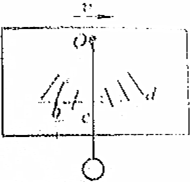 如图所示,汽车后视镜下悬吊着一个小摆件,司机可根据摆件的摆角来估计汽车的加速度.已知刻度线c位于O的竖直线上,∠bOc=30°,∠cOd=45°,若取g=10m/s2,当汽车水平向右行驶时( )
如图所示,汽车后视镜下悬吊着一个小摆件,司机可根据摆件的摆角来估计汽车的加速度.已知刻度线c位于O的竖直线上,∠bOc=30°,∠cOd=45°,若取g=10m/s2,当汽车水平向右行驶时( )| A. | 若细绳稳定地指示在c处,则说明汽车在匀速行驶 | |
| B. | 若细绳稳定地指示在b处,则说明汽车在匀加速行驶 | |
| C. | 若细绳稳定地指示在b处,则0.5s内汽车速度增大了5m/s | |
| D. | 若细绳稳定地指示在d处,则0.5s内汽车速度减小了5m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,木板A质量mA=1kg,足够长的木板B质量mB=4kg,质量为mC=4kg的木板C置于木板B上,水平地面光滑,B.C之间存在摩擦,开始时B.C均静止,现使A以v0=12m/s的初速度向右运动,与B碰撞后以4m/s的速度弹回,碰撞时间极短.(g=10m/s2),
如图所示,木板A质量mA=1kg,足够长的木板B质量mB=4kg,质量为mC=4kg的木板C置于木板B上,水平地面光滑,B.C之间存在摩擦,开始时B.C均静止,现使A以v0=12m/s的初速度向右运动,与B碰撞后以4m/s的速度弹回,碰撞时间极短.(g=10m/s2),查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 曲线运动,加速度的大小和方向均不变,是匀变速曲线运动 | |
| B. | 曲线运动,加速度的大小不变,方向改变,是非匀变速曲线运动 | |
| C. | 曲线运动,加速度的大小和方向均改变,是非匀变速曲线运动 | |
| D. | 若水平抛出是匀变速曲线运动,斜向上抛出则是非匀变速曲线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 无论水平面光滑与否,都有W1=W2 | B. | 若水平面光滑,则W1>W2 | ||
| C. | 若水平面粗糙,则W1<W2 | D. | 若水平面粗糙,则W1=W2 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
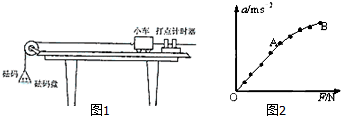
| A.小车与木板之间存在摩擦 | B.长木板保持了水平状态 |
| C.所挂砝码的总质量太大 | D.所用小车的质量太大. |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 已知飞船运动的轨道半径、周期以及引力常量,可算出飞船的质量 | |
| B. | 飞船绕地球沿圆轨道运动的速度比同步卫星的速度大,运动周期比同步卫星周期小 | |
| C. | 宇航员在飞船上处于完全失重状态,测力计、压强计、天平等都不能正常使用 | |
| D. | 若有两个这样的飞船在同一轨道上,相隔一段距离一前一后沿同一方向绕行,只要后一飞船向后喷气加速,则两飞船一定能实现对接 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com