
 如图所示的直角坐标系中,第I象限内存在沿y轴负向的匀强电场,第Ⅲ、Ⅳ象限内存在垂直于纸面向外的匀强磁场,磁感应强度为B.一带正电粒子M在y轴上的P点沿x轴正向射入电场,偏出电场后经x轴上的Q点进入磁场,再经磁场偏转后恰能回到原点O.已知M粒子经过Q点时的速度大小为v,方向与x轴成30°角,粒子的电量为q,质量为m,不计重力.求:
如图所示的直角坐标系中,第I象限内存在沿y轴负向的匀强电场,第Ⅲ、Ⅳ象限内存在垂直于纸面向外的匀强磁场,磁感应强度为B.一带正电粒子M在y轴上的P点沿x轴正向射入电场,偏出电场后经x轴上的Q点进入磁场,再经磁场偏转后恰能回到原点O.已知M粒子经过Q点时的速度大小为v,方向与x轴成30°角,粒子的电量为q,质量为m,不计重力.求:分析 (1)M粒子在电场中做类平抛运动,水平方向作匀速直线运动,竖直方向作匀加速直线运动,由速度的分解可求得入射速度.
(2)M粒子在磁场中做匀速圆周运动,由洛伦兹力充当向心力,由牛顿第二定律求出轨迹半径,由几何关系求出OQ间的距离.再研究其电场中的运动情况,由牛顿第二定律和竖直分速度公式结合,可求出匀强电场的场强大小.
(3)N粒子先经过电场加速,再进入磁场中偏转,先由动能定理求出加速获得的速度,再画出两个粒子在磁场中的轨迹,由几何关系得到轨迹的交点,即它们在磁场中的相遇点,找到磁场中轨迹对应的圆心角,可求出磁场中运动时间,再结合电场中运动时间,即可求解.
解答  解:(1)M粒子在电场中做类平抛运动,由速度分解可得:vP=vcos30°=$\frac{\sqrt{3}}{2}$v
解:(1)M粒子在电场中做类平抛运动,由速度分解可得:vP=vcos30°=$\frac{\sqrt{3}}{2}$v
(2)M粒子在磁场中运动时,有 qvB=m$\frac{{v}^{2}}{R}$,得:R=$\frac{mv}{qB}$
设OQ间的距离为L,由几何关系可得:
L=2Rsin30°=R=$\frac{mv}{qB}$
在电场中,有:L=vPt,vy=vsin30°=at
由牛顿第二定律得:qE=ma
联立可得:E=$\frac{\sqrt{3}}{4}$Bv
(3)N粒子,在电场中,由动能定理得:
qEL=$\frac{1}{2}mv{′}^{2}$
又L=$\frac{2\sqrt{3}mv}{3qB}$,且 L=$\frac{mv}{qB}$
可得:v′=v
两个粒子在磁场中的半径和OQ的长度均相等,且N粒子垂直x轴射入磁场,则其轨迹圆心在O点,如图,由几何关系可知,二者的轨迹相遇点、入射点Q和两个圆心四个点正好构成一个菱形,且有一个角为120°.
两个粒子在磁场中运动的周期为 T=$\frac{2πm}{qB}$
M粒子到相遇点的时间为:tM=$\frac{L}{{v}_{P}}$+$\frac{2}{3}$T=$\frac{L}{{v}_{P}}$+$\frac{4πm}{3qB}$
N粒子到相遇点的时间为:tN=$\frac{2L}{v′}$+$\frac{1}{3}$T=$\frac{2L}{v′}$+$\frac{2πm}{3qB}$
则△t=tM-tN=$\frac{2πm}{3qB}$-$\frac{2\sqrt{3}m}{3qB}$=(2π-2$\sqrt{3}$)$\frac{m}{3qB}$
即N粒子需要在M粒子离开P点后(2π-2$\sqrt{3}$)$\frac{m}{3qB}$时间释放.
答:(1)M粒子在P点的入射速度为$\frac{\sqrt{3}}{2}$v.
(2)匀强电场的场强大小为$\frac{\sqrt{3}}{4}$Bv.
(3)N粒子需要在M粒子离开P点后(2π-2$\sqrt{3}$)$\frac{m}{3qB}$时间释放.
点评 本题考查了带电粒子在电场和磁场中的运动,要掌握处理类平抛运动的方法:运动的分解法,抓住等时性结合运动学公式进行求解.对于粒子在磁场中的运动,会确定圆心、半径和圆心角,根据圆心角来确定磁场中运动时间.


科目:高中物理 来源: 题型:解答题
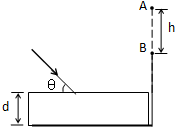 如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.保留两位有效数字.试求:
如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.保留两位有效数字.试求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,实线为一列正弦波在某一时刻的波形曲线,经过△t=0.7s,其波形如图中虚线所示,T<△t<2T.下列说法正确的是( )
如图所示,实线为一列正弦波在某一时刻的波形曲线,经过△t=0.7s,其波形如图中虚线所示,T<△t<2T.下列说法正确的是( )| A. | 波一定向右传播 | |
| B. | 波速和周期可能为0.5m/s和0.56s | |
| C. | 波速和周期可能为0.7m/s和0.40s | |
| D. | 该波遇到大小为0.2m的障碍物,可以发生明显衍射 | |
| E. | 观察者以某一速度向波源靠近时,接收到的频率可能为1.5 Hz |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 地球近地卫星做匀速圆周运动的线速度为ωR | |
| B. | 地球近地卫星做匀速圆周运动的线速度为$\sqrt{\frac{GM}{R}}$ | |
| C. | 地球同步卫星的运行速度大小为ω(R+h) | |
| D. | 地球同步卫星的运行速度大小为$\sqrt{\frac{GM}{R+h}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,倾角θ=30°、宽为L=1m的足够长的U形光滑金属导轨固定在磁感应强度B=1T、范围足够大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行于导轨的F牵引一根质量m=0.2kg、电阻R=1Ω的导体棒ab由静止开始沿导轨向上滑动;牵引力的功率恒定为P=90W,经过t=2s导体棒刚达到稳定速度v时棒上滑的距离s=11.9m.导体棒ab始终垂直导轨且与导轨接触良好,不计导轨电阻及一切摩擦,取g=10m/s2.求:
如图所示,倾角θ=30°、宽为L=1m的足够长的U形光滑金属导轨固定在磁感应强度B=1T、范围足够大的匀强磁场中,磁场方向垂直导轨平面斜向上.现用一平行于导轨的F牵引一根质量m=0.2kg、电阻R=1Ω的导体棒ab由静止开始沿导轨向上滑动;牵引力的功率恒定为P=90W,经过t=2s导体棒刚达到稳定速度v时棒上滑的距离s=11.9m.导体棒ab始终垂直导轨且与导轨接触良好,不计导轨电阻及一切摩擦,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在均匀介质中,各质点的平衡位置在同一水平直线上,相邻两质点的距离均为a,如图所示,振动从质点1开始向右传播,经过时间t,前11个质点第一次形成如图所示的波形,则此波的最大可能波速为( )
在均匀介质中,各质点的平衡位置在同一水平直线上,相邻两质点的距离均为a,如图所示,振动从质点1开始向右传播,经过时间t,前11个质点第一次形成如图所示的波形,则此波的最大可能波速为( )| A. | $\frac{17a}{t}$ | B. | $\frac{16a}{t}$ | C. | $\frac{12a}{t}$ | D. | $\frac{10a}{t}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com