
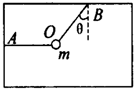
 如图所示,在长方体箱子内,用水平绳子AO和倾斜绳BO把质量为m的小球系于O点,箱子处于静止状态
如图所示,在长方体箱子内,用水平绳子AO和倾斜绳BO把质量为m的小球系于O点,箱子处于静止状态 ,
, =FB,故当箱子突然向左加速时BO绳弹力不变,故B错误.
=FB,故当箱子突然向左加速时BO绳弹力不变,故B错误.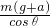 >FB
>FB

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中物理 来源: 题型:
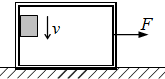 如图所示,质量为M=4.0kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右运动,铁箱与水平面间的动摩擦因数为μ1=0.20.这时铁箱内一个质量为m=1.0kg的木块恰好能沿箱的后壁向下匀速下滑,木块与铁箱间的动摩擦因数为μ2=0.50.求水平拉力F的大小.(取g=10m/s2)
如图所示,质量为M=4.0kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右运动,铁箱与水平面间的动摩擦因数为μ1=0.20.这时铁箱内一个质量为m=1.0kg的木块恰好能沿箱的后壁向下匀速下滑,木块与铁箱间的动摩擦因数为μ2=0.50.求水平拉力F的大小.(取g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:
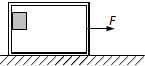 质量为M=2.5kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右匀加速运动,铁箱与水平面间的动摩擦因数为μ1=0.50.这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示),木块与铁箱内壁间的动摩擦因数为μ2=0.25.设最大静摩擦力等于滑动摩擦力,取g=10m/s2.求:
质量为M=2.5kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右匀加速运动,铁箱与水平面间的动摩擦因数为μ1=0.50.这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示),木块与铁箱内壁间的动摩擦因数为μ2=0.25.设最大静摩擦力等于滑动摩擦力,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
 质量为M=2.5kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右匀加速运动,铁箱与水平面间的动摩擦因数为μ1=0.50.这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示),木块与铁箱内壁间的动摩擦因数为μ2=0.25.设最大静摩擦力等于滑动摩擦力,取g=10m/s2.求:
质量为M=2.5kg的一只长方体形铁箱在水平拉力F作用下沿水平面向右匀加速运动,铁箱与水平面间的动摩擦因数为μ1=0.50.这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示),木块与铁箱内壁间的动摩擦因数为μ2=0.25.设最大静摩擦力等于滑动摩擦力,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
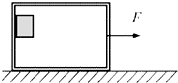 质量为M=2.5kg的一只长方体形状的铁箱在水平拉力F作用下沿水平面向右匀加速运动,铁箱与水平面间的动摩擦因数为μ1=0.50.这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示),木块与铁箱内壁间的动摩擦因数为μ2=0.25.设最大静摩擦力等于滑动摩擦力,g取10m/s2.求:
质量为M=2.5kg的一只长方体形状的铁箱在水平拉力F作用下沿水平面向右匀加速运动,铁箱与水平面间的动摩擦因数为μ1=0.50.这时铁箱内一个质量为m=0.5kg的木块恰好能静止在后壁上(如图所示),木块与铁箱内壁间的动摩擦因数为μ2=0.25.设最大静摩擦力等于滑动摩擦力,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
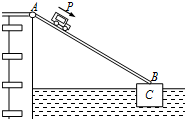 如图所示,质量为M、长度为L的均匀桥板AB,A端连在桥墩上可以自由转动,B端搁在浮在水面的方形浮箱C上,一辆质量为m的汽车P从A处匀速驰向B处,设浮箱为长方体,上下浮动时上表面保持水平,并始终在水面以上,上表面面积为S,水密度为ρ,汽车未上桥面时桥面与浮箱上表面的夹角为α,汽车在桥面上行驶的过程中,浮箱沉入水中的深度增加,求:
如图所示,质量为M、长度为L的均匀桥板AB,A端连在桥墩上可以自由转动,B端搁在浮在水面的方形浮箱C上,一辆质量为m的汽车P从A处匀速驰向B处,设浮箱为长方体,上下浮动时上表面保持水平,并始终在水面以上,上表面面积为S,水密度为ρ,汽车未上桥面时桥面与浮箱上表面的夹角为α,汽车在桥面上行驶的过程中,浮箱沉入水中的深度增加,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com