
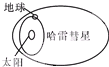
 地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆.天文学家哈雷曾经在1682年跟踪观测过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍(如图),并预言这颗彗星将每隔一定时间就会出现.哈雷的预言得到证实,该彗星被命名为哈雷彗星.哈雷彗星最近出现的时间是1986年,请你根据开普勒行星运动第三定律估算,它下次飞近地球大约在
地球的公转轨道接近圆,但彗星的运动轨道则是一个非常扁的椭圆.天文学家哈雷曾经在1682年跟踪观测过一颗彗星,他算出这颗彗星轨道的半长轴约等于地球公转半径的18倍(如图),并预言这颗彗星将每隔一定时间就会出现.哈雷的预言得到证实,该彗星被命名为哈雷彗星.哈雷彗星最近出现的时间是1986年,请你根据开普勒行星运动第三定律估算,它下次飞近地球大约在科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
(即![]() =k,其中T为行星绕太阳公转的周期,a为轨道的半长轴)估算,它下次飞近地球是哪一年?
=k,其中T为行星绕太阳公转的周期,a为轨道的半长轴)估算,它下次飞近地球是哪一年?
查看答案和解析>>
科目:高中物理 来源: 题型:

图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com