
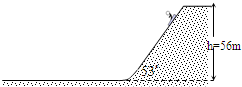
 南戴河旅游区,有一项滑沙游戏,滑沙场是在水平沙滩上筑起了一个大沙坡,如图所示.游戏开始,滑沙者在坡顶处坐在一个平板滑沙车上,然后由工作人员推动一下,使滑沙者乘坐平板车沿坡滑下.设斜坡高度为56m,倾角为53°,滑沙车与沙之间的动摩擦因数为0.4,滑沙者起动时初速度很小可忽略不计,重力加速度g取10m/s2,其中sin53°=0.8,cos53°=0.6.求:(1)滑沙者在滑沙过程中的运动时间.
南戴河旅游区,有一项滑沙游戏,滑沙场是在水平沙滩上筑起了一个大沙坡,如图所示.游戏开始,滑沙者在坡顶处坐在一个平板滑沙车上,然后由工作人员推动一下,使滑沙者乘坐平板车沿坡滑下.设斜坡高度为56m,倾角为53°,滑沙车与沙之间的动摩擦因数为0.4,滑沙者起动时初速度很小可忽略不计,重力加速度g取10m/s2,其中sin53°=0.8,cos53°=0.6.求:(1)滑沙者在滑沙过程中的运动时间. =
= a1t12得,
a1t12得,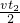 =98m
=98m

 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中物理 来源: 题型:
 南戴河旅游区,有一项滑沙游戏,滑沙场是在水平沙滩上筑起了一个大沙坡,如图所示.游戏开始,滑沙者在坡顶处坐在一个平板滑沙车上,然后由工作人员推动一下,使滑沙者乘坐平板车沿坡滑下.设斜坡高度为56m,倾角为53°,滑沙车与沙之间的动摩擦因数为0.4,滑沙者起动时初速度很小可忽略不计,重力加速度g取10m/s2,其中sin53°=0.8,cos53°=0.6.求:(1)滑沙者在滑沙过程中的运动时间.
南戴河旅游区,有一项滑沙游戏,滑沙场是在水平沙滩上筑起了一个大沙坡,如图所示.游戏开始,滑沙者在坡顶处坐在一个平板滑沙车上,然后由工作人员推动一下,使滑沙者乘坐平板车沿坡滑下.设斜坡高度为56m,倾角为53°,滑沙车与沙之间的动摩擦因数为0.4,滑沙者起动时初速度很小可忽略不计,重力加速度g取10m/s2,其中sin53°=0.8,cos53°=0.6.求:(1)滑沙者在滑沙过程中的运动时间.查看答案和解析>>
科目:高中物理 来源: 题型:
 南戴河旅游区,有一项滑沙游戏,滑沙场是在水平沙滩上筑起了一个大沙坡,如图所示.游戏开始,滑沙者在坡顶处坐在一个平板滑沙车上,然后由工作人员推动一下,使滑沙者乘坐平板车沿坡滑下.设斜坡高度为56m,倾角为53°,滑沙车与沙之间的动摩擦因数为0.4,滑沙者起动时初速度很小可忽略不计,重力加速度g取10m/s2,其中sin53°=0.8,cos53°=0.6.求:滑沙者在滑沙过程中的运动时间.
南戴河旅游区,有一项滑沙游戏,滑沙场是在水平沙滩上筑起了一个大沙坡,如图所示.游戏开始,滑沙者在坡顶处坐在一个平板滑沙车上,然后由工作人员推动一下,使滑沙者乘坐平板车沿坡滑下.设斜坡高度为56m,倾角为53°,滑沙车与沙之间的动摩擦因数为0.4,滑沙者起动时初速度很小可忽略不计,重力加速度g取10m/s2,其中sin53°=0.8,cos53°=0.6.求:滑沙者在滑沙过程中的运动时间.查看答案和解析>>
科目:高中物理 来源:2011年江苏省无锡一中高考物理二轮复习卷(五)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com