
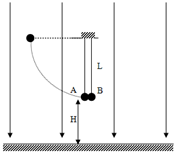
 在空间足够大的方向竖直向下的匀强电场中两长为L的绝缘细线并列上端固定,另一端悬挂质量分别为mA和mB的带正电小球,带电量分别为qA和qB,且有$\frac{{q}_{A}}{{m}_{A}}$=$\frac{{q}_{B}}{{m}_{B}}$=k.平衡时,两小球刚好相接触并无弹力,距地面高度为H,现将A球拉离至与悬点等高处,使细线绷直,由静止释放,当A摆至最低点时与B球发生弹性碰撞,刚碰撞完的瞬间,系B球的细线突然被拉断.(不计两球间的库仑力,已知电场强度为E.)求:
在空间足够大的方向竖直向下的匀强电场中两长为L的绝缘细线并列上端固定,另一端悬挂质量分别为mA和mB的带正电小球,带电量分别为qA和qB,且有$\frac{{q}_{A}}{{m}_{A}}$=$\frac{{q}_{B}}{{m}_{B}}$=k.平衡时,两小球刚好相接触并无弹力,距地面高度为H,现将A球拉离至与悬点等高处,使细线绷直,由静止释放,当A摆至最低点时与B球发生弹性碰撞,刚碰撞完的瞬间,系B球的细线突然被拉断.(不计两球间的库仑力,已知电场强度为E.)求:分析 (1)A向下运动的过程中重力和电场力做功,由动能定理即可求出A到达最低点的速度;
(2)两个小球在最低点受到重力和绳子的拉力、电场力,水平方向的动量守恒,由动量守恒即可求出碰撞后的速度,再分别由平抛运动与机械能守恒即可求出.
解答 解:(1)A向下运动的过程中重力和电场力做功,由动能定理得:
${m}_{A}gL+{q}_{A}E•L=\frac{1}{2}{m}_{A}{v}^{2}$
所以:v=$\sqrt{2gL+2kEL}$
(2)两个小球在最低点受到重力和绳子的拉力、电场力,水平方向A与B组成的系统的动量守恒,选取向右为正方向,则:
mAv=mAvA+mBvB
弹性碰撞的过程中机械能守恒,所以:
$\frac{1}{2}{m}_{A}{v}^{2}=\frac{1}{2}{m}_{A}{v}_{A}^{2}+\frac{1}{2}{m}_{B}{v}_{B}^{2}$
联立得:${v}_{A}=\frac{{m}_{B}-{m}_{A}}{{m}_{A}+{m}_{B}}•\sqrt{2gL+2kEL}$;${v}_{B}=\frac{2{m}_{A}}{{m}_{A}+{m}_{B}}•\sqrt{2gL+2kEL}$.
碰撞后A做单摆运动,机械能守恒,到达最高点时:
${m}_{A}gh+{q}_{A}E•h=\frac{1}{2}{m}_{A}{v}_{A}^{2}$
所以:h=$\frac{{v}_{A}^{2}}{2(g+kE)}$=($\frac{{m}_{B}-{m}_{A}}{{m}_{A}+{m}_{B}}$)2•L
由题意B做类平抛运动,竖直方向的加速度:
a=$\frac{{m}_{B}g+{q}_{B}E}{{m}_{B}}=\frac{{m}_{B}g+k{m}_{B}E}{{m}_{B}}=g+kE$
竖直方向:H=$\frac{1}{2}a{t}^{2}$,水平方向:X=vBt
联立得:X=$\frac{2{m}_{A}}{{m}_{A}+{m}_{B}}•\sqrt{2HL}$
答:(1)A与B碰撞前瞬间的速度大小是$\sqrt{2gL+2kEL}$.
(2)B球落地点到悬点的水平距离是$\frac{2{m}_{A}}{{m}_{A}+{m}_{B}}•\sqrt{2HL}$,A球碰撞后上升的最大高度是($\frac{{m}_{B}-{m}_{A}}{{m}_{A}+{m}_{B}}$)2•L.
点评 该题数据竖直平面内的圆周运动、动量守恒动量以及类平抛运动等,涉及的过程多,物理量多,在解答的过程中要细心.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
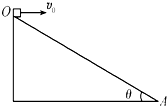 如图所示,足够长斜面OA的倾角为θ,固定在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中与斜面之间的最远距离( )•
如图所示,足够长斜面OA的倾角为θ,固定在水平地面上,现从顶点O以速度v0平抛一小球,不计空气阻力,重力加速度为g,求小球在飞行过程中与斜面之间的最远距离( )•| A. | $\frac{{v}_{0}sinθ}{2g}$ | B. | $\frac{{{v}_{0}}^{2}}{2g}$ | ||
| C. | $\frac{{{v}_{0}}^{2}sinθ}{2gcosθ}$ | D. | $\frac{{{v}_{0}}^{2}si{n}^{2}θ}{2gcosθ}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 重心就是物体上最重的点 | |
| B. | 用一根细线悬挂的物体静止时,细线方向一定通过重心 | |
| C. | 重心的位置不一定在物体上,但形状规则的、质量分布均匀的物体的重心一定在物体上 | |
| D. | 质量分布均匀、形状规则的物体,它的重心在几何中心 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
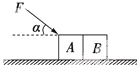 如图所示,物体A、B与地面间动摩擦因数相同,质量也相同,在力F的作用下一起沿水平地面运动了距离s,以下说法中正确的是( )
如图所示,物体A、B与地面间动摩擦因数相同,质量也相同,在力F的作用下一起沿水平地面运动了距离s,以下说法中正确的是( )| A. | 摩擦力对A、B所做的功相同 | B. | 合外力对A、B所做的功相同 | ||
| C. | F对A所做的功与A对B做的功相同 | D. | A对B的作用力大于B对A的作用力 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com