
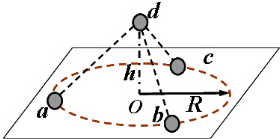
 ��ͼ��ʾ��a��b��c��d�ĸ�������Ϊm�Ĵ���С��ǡ�ù��ɡ����ǹ��¡�֮�Σ�����a��b��c����ȫ��ͬ�Ĵ���С���ڹ⻬��Եˮƽ���ڵ�ͬһԲ������O�����뾶ΪR������Բ���˶�����С������λ��ǡ�ý�Բ�ܵȷ֣�С��dλ��O�����Ϸ�h������������F������ǡ���ھ�ֹ״̬����֪a��b��c��С��ĵ������Ϊq��d��ĵ����Ϊ6q��h=$\sqrt{2}$R���������ٶ�Ϊg������������Ϊk��������
��ͼ��ʾ��a��b��c��d�ĸ�������Ϊm�Ĵ���С��ǡ�ù��ɡ����ǹ��¡�֮�Σ�����a��b��c����ȫ��ͬ�Ĵ���С���ڹ⻬��Եˮƽ���ڵ�ͬһԲ������O�����뾶ΪR������Բ���˶�����С������λ��ǡ�ý�Բ�ܵȷ֣�С��dλ��O�����Ϸ�h������������F������ǡ���ھ�ֹ״̬����֪a��b��c��С��ĵ������Ϊq��d��ĵ����Ϊ6q��h=$\sqrt{2}$R���������ٶ�Ϊg������������Ϊk��������| A�� | С��aһ�������� | |
| B�� | С��b������Ϊ$\frac{2��R}{q}$$\sqrt{\frac{mR}{k}}$ | |
| C�� | С��c�ļ��ٶȴ�СΪ$\frac{\sqrt{3}k{q}^{2}}{3m{R}^{2}}$ | |
| D�� | ����F��ֱ���ϣ���С����mg+$\frac{2\sqrt{6}k{q}^{2}}{{R}^{2}}$ |
���� a��b��c��������С����ˮƽ����������Բ���˶����ɺ������ṩ���������������������������ţ�ٵڶ������о����ɣ�
��� �⣺A��a��b��c��С�������������ͬ��Ҫʹ����������Բ���˶���d����a��b��c��С��һ�������ֵ�ɣ�����d��ĵ���δ֪������a��һ�������磬��A����
B���� db������ˮƽ����ļн�Ϊ������cos��=$\frac{R}{\sqrt{{h}^{2}+{R}^{2}}}$=$\frac{\sqrt{3}}{3}$��sin��=$\frac{h}{\sqrt{{h}^{2}+{R}^{2}}}$=$\frac{\sqrt{6}}{3}$
��b����ţ�ٵڶ����ɺ��������ã�k$\frac{6q•q}{{h}^{2}+{R}^{2}}$cos��-2k$\frac{{q}^{2}}{��2Rcos30�㣩^{2}}$cos30��=m$\frac{4{��}^{2}}{{T}^{2}}$R=ma
��ã�T=$\frac{2��R}{q}$$\sqrt{\frac{\sqrt{3}mR}{k}}$��a=$\frac{\sqrt{3}k{q}^{2}}{3m{R}^{2}}$
��С��c�ļ��ٶȴ�СΪ$\frac{\sqrt{3}k{q}^{2}}{3m{R}^{2}}$����B����C��ȷ��
D����d����ƽ�������ã�F=3k$\frac{6q•q}{{h}^{2}+{R}^{2}}$sin��+mg=mg+$\frac{2\sqrt{6}k{q}^{2}}{{R}^{2}}$����D��ȷ��
��ѡ��CD
���� ������Բ�����ƣ��ؼ�Ҫ��ȷ�����ĸ�С��������ȷ������������Դ�ǹؼ�������ţ�ٵڶ����ɺ�ƽ�������о���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
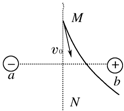 ��ͼ�У�a��b���������ֵ�ɣ�MNΪab���ߵ��д��ߣ�����һ���������Ӵ�M����һ�����ٶ�v0���룬��ʼʱһ�ι켣��ͼ��ʵ�ߣ������������������������й������ڷ�Խ�õ糡�����������е�˵������ȷ���ǣ�������
��ͼ�У�a��b���������ֵ�ɣ�MNΪab���ߵ��д��ߣ�����һ���������Ӵ�M����һ�����ٶ�v0���룬��ʼʱһ�ι켣��ͼ��ʵ�ߣ������������������������й������ڷ�Խ�õ糡�����������е�˵������ȷ���ǣ�������| A�� | �����Ӵ����� | |
| B�� | �����ӵĶ����������С | |
| C�� | ����������λ�õĵ����Ƚ��ͣ������� | |
| D�� | �������˶�������Զ�����ٶȵĴ�Сһ����Ϊv0 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���ڡ�̽��ƽ���˶����˶����ɡ���ʵ���У���������С��ƽ���˶��IJ��ֹ켣����֪ͼ��С����ı߳�ΪL����С��ƽ�ij��ٶ�v0=2$\sqrt{gL}$��b����ٶ�vb=$\frac{5}{2}\sqrt{gL}$������������L��g��ʾ��
��ͼ��ʾ���ڡ�̽��ƽ���˶����˶����ɡ���ʵ���У���������С��ƽ���˶��IJ��ֹ켣����֪ͼ��С����ı߳�ΪL����С��ƽ�ij��ٶ�v0=2$\sqrt{gL}$��b����ٶ�vb=$\frac{5}{2}\sqrt{gL}$������������L��g��ʾ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
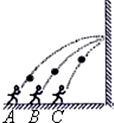 ������һ�ֶ�ǽ����������˶�����ͼ��ʾ��һͬѧ�ֱ���ͬһֱ���ϵ�A��B��C����λ�û�����������ֱ����ǽ��ͬһλ�ã���ɳ����ٶȷֱ�Ϊv1��v2��v3�������α�������ĸ߶Ⱦ���ͬ����ɳ��ķ�����ˮƽ����нǷֱ�Ϊ��1����2����3��������˵����ȷ���ǣ�������
������һ�ֶ�ǽ����������˶�����ͼ��ʾ��һͬѧ�ֱ���ͬһֱ���ϵ�A��B��C����λ�û�����������ֱ����ǽ��ͬһλ�ã���ɳ����ٶȷֱ�Ϊv1��v2��v3�������α�������ĸ߶Ⱦ���ͬ����ɳ��ķ�����ˮƽ����нǷֱ�Ϊ��1����2����3��������˵����ȷ���ǣ�������| A�� | v1��v2��v3 | B�� | ��1����2����3 | C�� | v1��v2��v3 | D�� | ��1����2����3 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����Զ�λ��������ѧ�����Ͽ� | |
| B�� | ����ͬ�����ǵĽ��ٶ��䱻ȷ�������߶Ⱥ����ٶȿ���ѡ�߶����ӣ����ٶȼ�С���߶Ƚ��ͣ����ٶ����� | |
| C�� | �����е����ٶ�һ��С�ڵ�һ�����ٶ� | |
| D�� | �����е����ٶ�һ�����ڵ�һ�����ٶȺ͵ڶ������ٶ�֮�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ķ�����ֵ��ӣ�����ԭ�Ӿ��к�ʽ�ṹ | |
| B�� | ���ղ������ۣ���ԭ�Ӻ�����ӴӰ뾶��С�Ĺ��ԾǨ���뾶�ϴ�Ĺ��ʱ�����ӵĶ��ܼ�С��ԭ������������ | |
| C�� | 뱵İ�˥��Ϊ3.8�죬����4���ԭ�Ӻˣ�����7.6���ֻʣ��1�� | |
| D�� | ̫�������������Ҫ����̫���ڲ��ĺ��ѱ䷴Ӧ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
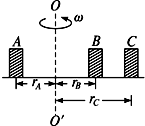 ��ͼ��ʾ��A��B��C����С�������ˮƽ��ת��Բ���ϣ�������Բ�̼�����Ħ�����������������ȣ�����ϵ����Ϊk����֪mA=2mB=2mC��rC=2rA=2rB��Բ̨�Խ��ٶȦ���תʱ��A��B��C��û�л�����������
��ͼ��ʾ��A��B��C����С�������ˮƽ��ת��Բ���ϣ�������Բ�̼�����Ħ�����������������ȣ�����ϵ����Ϊk����֪mA=2mB=2mC��rC=2rA=2rB��Բ̨�Խ��ٶȦ���תʱ��A��B��C��û�л�����������| A�� | C�����ļ��ٶ���� | |
| B�� | B���ܾ�Ħ������� | |
| C�� | ��Բ��ת��������ʱ��C��B�ȿ�ʼ���� | |
| D�� | ��Բ��ת��������ʱ��A��B�ȿ�ʼ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
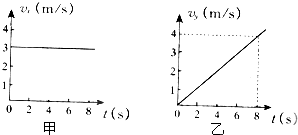
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
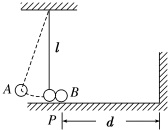 ��ͼ��ʾ����һ���ڳ�Ϊl�ĵ��ڣ��ֽ�����A����ƽ��λ��һ����С�ĽǶȣ�Ȼ���ɾ�ֹ�ͷţ�A����ƽ��λ��Pʱ��ǡ�뾲ֹ��P����B������ײ������A�������Ұڶ���B�����ٶ�v�ع⻬ˮƽ�������˶������Ҳ��ǽ����ײ����ԭ���ʷ��أ���B�����»ص�λ��Pʱ����A�ٴ���������λ��P��ǽ�ڼ�ľ���d����Ϊ��������
��ͼ��ʾ����һ���ڳ�Ϊl�ĵ��ڣ��ֽ�����A����ƽ��λ��һ����С�ĽǶȣ�Ȼ���ɾ�ֹ�ͷţ�A����ƽ��λ��Pʱ��ǡ�뾲ֹ��P����B������ײ������A�������Ұڶ���B�����ٶ�v�ع⻬ˮƽ�������˶������Ҳ��ǽ����ײ����ԭ���ʷ��أ���B�����»ص�λ��Pʱ����A�ٴ���������λ��P��ǽ�ڼ�ľ���d����Ϊ��������| A�� | $\frac{��v}{4}\sqrt{\frac{l}{g}}$ | B�� | $\frac{��v}{2}\sqrt{\frac{l}{g}}$ | C�� | $\frac{3��v}{4}\sqrt{\frac{l}{g}}$ | D�� | ��v$\sqrt{\frac{l}{g}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com