
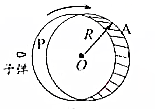
 如图是一种测定子弹速度的装置,它时用一种薄片材料做成的圆筒,其半径为R,圆筒绕中心轴以N圈/秒转速转动.一颗子弹垂直于圆筒中心轴线入射,并且在筒内经过中心轴线上的O点,如果子弹穿过圆筒时在墙壁上只留下一个弹孔,则子弹的速度表达式为v=$\frac{2rω}{(2k+1)π}$,k=0、1、2、3…(重力的影响和空气阻力不计,子弹穿过圆筒壁时速度变化不计,用k表示非负整数,即k=0,1,2,3…)
如图是一种测定子弹速度的装置,它时用一种薄片材料做成的圆筒,其半径为R,圆筒绕中心轴以N圈/秒转速转动.一颗子弹垂直于圆筒中心轴线入射,并且在筒内经过中心轴线上的O点,如果子弹穿过圆筒时在墙壁上只留下一个弹孔,则子弹的速度表达式为v=$\frac{2rω}{(2k+1)π}$,k=0、1、2、3…(重力的影响和空气阻力不计,子弹穿过圆筒壁时速度变化不计,用k表示非负整数,即k=0,1,2,3…) 分析 子弹沿圆筒直径穿过圆筒,结果发现子弹穿过圆筒时在墙壁上只留下一个弹孔,在子弹飞行的时间内,圆筒转动的角度为(2k+1)π,k=0、1、2、3…,结合角速度求出时间,从而得出子弹的速度.
解答 解:子弹穿过圆筒时在墙壁上只留下一个弹孔,则在子弹飞行的时间内,圆筒转动半周,或k+$\frac{1}{2}$周,转过的角度为(2k+1)π,k=0、1、2、3…,
则时间t=$\frac{(2k+1)π}{ω}$,
所以子弹的速度v=$\frac{2r}{t}$=$\frac{2rω}{(2k+1)π}$,k=0、1、2、3…,
故答案为:v=$\frac{2rω}{(2k+1)π}$,k=0、1、2、3….
点评 解决本题的关键知道圆筒转动的周期性,结合转过角度的通项式得出运动的时间,抓住子弹飞行的时间和圆筒转动时间相等进行求解.


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 大量的光子中有些光子表现出波动性,有些光子表现出粒子性 | |
| B. | 光在传播时是波,而与物质相互作用时就转变成粒子 | |
| C. | 高频光是粒子,低频光是波 | |
| D. | 波粒二象性是光的属性,有时它的波动性显著,有时它的粒子性显著 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过,R=0.10Ω,轨道相距L=0.5m,B=0.6T,v=2m/s.问:
如图所示,导体AB在做切割磁感线运动时,将产生一个电动势,因而在电路中有电流通过,R=0.10Ω,轨道相距L=0.5m,B=0.6T,v=2m/s.问:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量m=20kg的物体放在水平地面上,现给物体施加一个与水平面成θ=37°角的斜向上的F=50N的作用力.取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,质量m=20kg的物体放在水平地面上,现给物体施加一个与水平面成θ=37°角的斜向上的F=50N的作用力.取g=10m/s2,sin37°=0.6,cos37°=0.8,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,是在同一轨道平面上运行的三颗不同的人造地球卫星,关于各相关物理量的关系,下列说法正确的是( )
如图所示,是在同一轨道平面上运行的三颗不同的人造地球卫星,关于各相关物理量的关系,下列说法正确的是( )| A. | 根据v=$\sqrt{gr}$,可知线速度vA<vB<vC | |
| B. | 根据万有引力定律可知,所受的万有引力关系为FA>FB>FC | |
| C. | 角速度的关系为ωA>ωB>ωC | |
| D. | 向心加速度的关系为aA<aB<aC |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
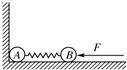 质量均为m的A、B两个小球之间系一根质量不计的弹簧,放在光滑的水平面上.A紧靠墙壁,如图所示.今用力F将B球向左挤压弹簧达到平衡时,在突然将力F撤去的瞬间( )
质量均为m的A、B两个小球之间系一根质量不计的弹簧,放在光滑的水平面上.A紧靠墙壁,如图所示.今用力F将B球向左挤压弹簧达到平衡时,在突然将力F撤去的瞬间( )| A. | A球加速度的大小为$\frac{F}{2m}$ | B. | A球加速度的大小为$\frac{F}{m}$ | ||
| C. | B球加速度的大小为$\frac{F}{2m}$ | D. | B球加速度的大小为$\frac{F}{m}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com