

���� ��1������ƽ���˶���ˮƽ�������ֱ�����ϵ��˶����ɵó�y��x�Ĺ�ϵʽ���Ӷ�ȷ����ȷ��ͼ�ߣ�
��2��ƽ���˶�����ֱ�����������������˶�������λ��ʱ�乫ʽ�ֱ�����ų�ĵ�A��B�����ʱ�䣬�Ӷ��ó�A��B��ʱ�䣬���A��B��ˮƽλ�����С��ij��ٶȣ������ٶ�λ�ƹ�ʽ���C���ķ��ٶȣ����ƽ���ı��ζ������C����ٶȴ�С��
��� �⣺��1������x=v0t��y=$\frac{1}{2}g{t}^{2}$�ã�y=$\frac{1}{2}g\frac{{x}^{2}}{{{v}_{0}}^{2}}$����֪y��x2��ͼ��Ϊ��ԭ�����бֱ�ߣ���ѡ��C��
��2������${y}_{1}=\frac{1}{2}g{{t}_{1}}^{2}$�ã�${t}_{1}=\sqrt{\frac{2{y}_{1}}{g}}=\sqrt{\frac{2��0.05}{10}}s=0.1s$��
����${y}_{2}=\frac{1}{2}g{{t}_{2}}^{2}$�ã�${t}_{2}=\sqrt{\frac{2{y}_{2}}{g}}$=$\sqrt{\frac{2��0.45}{10}}s=0.3s$��
��֪A��B��ʱ���t=t2-t1=0.3-0.1s=0.2s��ƽ���˶��ij��ٶ�${v}_{0}=\frac{��x}{��t}=\frac{0.4}{0.2}m/s=2.0m/s$��
C�����ֱ���ٶ�${v}_{yc}=\sqrt{2g{y}_{3}}=\sqrt{2��10��0.6}$m/s=$2\sqrt{3}$m/s��
����ƽ���ı��ζ���֪��C����ٶ�${v}_{c}=\sqrt{{{v}_{0}}^{2}+{{v}_{yc}}^{2}}$=$\sqrt{4+12}$m/s=4.0m/s��
�ʴ�Ϊ����1��C����2��2.0��4.0��
���� �������Ĺؼ�֪��ƽ���˶���ˮƽ�������ֱ�����ϵ��˶����ɣ�����˶�ѧ��ʽ�����������⣬�ѶȲ���


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��10tʱ���ʵ���ٶȴ�СΪ11at | |
| B�� | ��10tʱ���ʵ���ٶȴ�СΪ66at | |
| C�� | ��10tʱ�����ʵ�ͨ������λ��Ϊ385at2 | |
| D�� | ��10tʱ�����ʵ��ƽ���ٶȴ�СΪ$\frac{77}{4}$at |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���������ķ������Ǵ�ֱ�ڴų��ķ��� | |
| B�� | ���������ķ�����Բ���ֱ�ڴ������ӵ��˶����� | |
| C�� | ���������Ĵ�С��������ӵ��ٶȷ���ʹų�����ļн��� | |
| D�� | �����������ӵ��ٶȼ��룬���������Ĵ�С��Ϊԭ����һ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��֪�����Ƶ��ݳ���Ϊ0.7eV����ԭ�ӵ��ܼ�ͼ��ͼ��ʾ��һȺ��ԭ�Ӵ���������4�ܼ�״̬������ԭ�ӿ��ܷ���6��Ƶ�ʵĹ��ӣ���5��Ƶ�ʵķ��������ʹ�Ʒ������ЧӦ���ӽ����Ʊ����ݳ��Ĺ���ӵ���������Ϊ12.05eV��
��֪�����Ƶ��ݳ���Ϊ0.7eV����ԭ�ӵ��ܼ�ͼ��ͼ��ʾ��һȺ��ԭ�Ӵ���������4�ܼ�״̬������ԭ�ӿ��ܷ���6��Ƶ�ʵĹ��ӣ���5��Ƶ�ʵķ��������ʹ�Ʒ������ЧӦ���ӽ����Ʊ����ݳ��Ĺ���ӵ���������Ϊ12.05eV���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
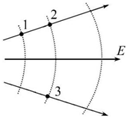
| A�� | ͬһ�����1��2��������ܵ糡����ͬ | |
| B�� | ͬһ�����2��3��������ܵ糡����ͬ | |
| C�� | ����ɴӵ�1�˶�����2���糡�������� | |
| D�� | ����ɴӵ�1�˶�����2�ʹӵ�1�˶�����3�����ӵĵ�������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ�������ε����߿�abcd�ı߳�ΪL��ÿ�ߵ����Ϊr���߿��ڴŸ�Ӧǿ��ΪB����ǿ�ų����Խ��ٶȦ���cd���ͼʾλ�ÿ�ʼ����ת����ת����Ÿ��ߴ�ֱ��һ�����ѹ���õ�ˢ�����߿��c��d�����ϣ�����˵���в���ȷ���ǣ�������
��ͼ��ʾ�������ε����߿�abcd�ı߳�ΪL��ÿ�ߵ����Ϊr���߿��ڴŸ�Ӧǿ��ΪB����ǿ�ų����Խ��ٶȦ���cd���ͼʾλ�ÿ�ʼ����ת����ת����Ÿ��ߴ�ֱ��һ�����ѹ���õ�ˢ�����߿��c��d�����ϣ�����˵���в���ȷ���ǣ�������| A�� | ��ѹ������Ϊ$\frac{\sqrt{2}}{2}$B��L2 | |
| B�� | ��ѹ������Ϊ$\frac{\sqrt{2}}{8}$B��L2 | |
| C�� | ��ͼʾλ�ÿ�ʼ��ʱ�������߿������˲ʱֵ����ʽΪi=$\frac{B��{L}^{2}}{4r}$sin��t | |
| D�� | �߿��ͼʾλ��ת��$\frac{��}{2}$�Ĺ����У�����cd�ߵĵ����Ϊq=$\frac{B{L}^{2}}{r}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���������䵽����п�����ʱ�ܷ������ЧӦ�������������ߵ�����ǿ��ʱ����п������ݳ��Ĺ���ӵ���������Ҳ��֮���� | |
| B�� | ������Ϊ��ԭ���е��ӹ�������ӻ��ģ�����Ҳ�����ӻ��� | |
| C�� | .��������ԭ�Ӻ�����Ӹ����˶��γɵ� | |
| D�� | ���Ӳ�������������Ҳ���ж��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ������ͼ��·������Դ�綯��E ������Rx����ֵ��ͼ�е���R ����ֵ��֪��K2Ϊ����˫�����أ�VΪ�����ѹ����EΪ��Դ�����費�ɺ��ԣ���
������ͼ��·������Դ�綯��E ������Rx����ֵ��ͼ�е���R ����ֵ��֪��K2Ϊ����˫�����أ�VΪ�����ѹ����EΪ��Դ�����費�ɺ��ԣ����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com