
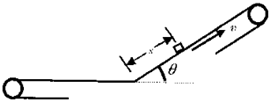
 如图所示,运输带由水平和倾斜两部分组成,倾斜部分倾角θ=37°.运输带运行速度v=1m/s,方向如图箭头所示.有一小块颜料落在倾斜部分上,下落在运输带上的地点与倾斜部分底端距离s=1.0m.已知颜料与运输带之间的动摩擦因数μ=0.5,则颜料从下滑到再次上升到最高点的过程中,在皮带上留下的痕迹有多长?(设颜料通过运输带两部分交接处速度大小不变,g取10m/s2)
如图所示,运输带由水平和倾斜两部分组成,倾斜部分倾角θ=37°.运输带运行速度v=1m/s,方向如图箭头所示.有一小块颜料落在倾斜部分上,下落在运输带上的地点与倾斜部分底端距离s=1.0m.已知颜料与运输带之间的动摩擦因数μ=0.5,则颜料从下滑到再次上升到最高点的过程中,在皮带上留下的痕迹有多长?(设颜料通过运输带两部分交接处速度大小不变,g取10m/s2)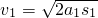 =2m/s
=2m/s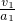 =1s
=1s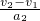 =0.6s
=0.6s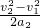 =0.3m
=0.3m =0.5s
=0.5s =0.25m
=0.25m

科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:单选题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
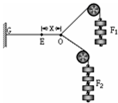 探究求合力的方法的实验中,把劲度系数为k的橡皮条GE的一端固定在板上的G点,橡皮条的另一端E拴上两条细绳,如图所示,两组钩码互成角度拉橡皮条GE使之伸长了EO长度,结点到达某一位置O;再用一条细绳挂上适当的钩码把橡皮条拉长,使结点也到达位置O,在本次实验中,两次把橡皮条拉到同一位置O的目的是________.若EO长度为x,橡皮筋由于形变产生的弹力大小为________.
探究求合力的方法的实验中,把劲度系数为k的橡皮条GE的一端固定在板上的G点,橡皮条的另一端E拴上两条细绳,如图所示,两组钩码互成角度拉橡皮条GE使之伸长了EO长度,结点到达某一位置O;再用一条细绳挂上适当的钩码把橡皮条拉长,使结点也到达位置O,在本次实验中,两次把橡皮条拉到同一位置O的目的是________.若EO长度为x,橡皮筋由于形变产生的弹力大小为________.查看答案和解析>>
科目:高中物理 来源: 题型:单选题
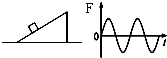 如图,斜面体M的底面粗糙,斜面光滑,放在粗糙水平面上.物块m放在斜面上,现对m施一平行于斜面的作用力F,F随时间的变化规律如图.若物块始终在斜面上运动,而斜面体一直保持静止,则地面对斜面体的摩擦力f与时间t的关系图象应是下图中的
如图,斜面体M的底面粗糙,斜面光滑,放在粗糙水平面上.物块m放在斜面上,现对m施一平行于斜面的作用力F,F随时间的变化规律如图.若物块始终在斜面上运动,而斜面体一直保持静止,则地面对斜面体的摩擦力f与时间t的关系图象应是下图中的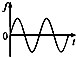
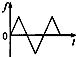
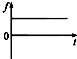
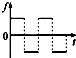
查看答案和解析>>
科目:高中物理 来源: 题型:单选题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com