
| A. | $\frac{R-d}{R+h}$ | B. | $\frac{(R-d)^{2}}{(R+h)^{2}}$ | C. | $\frac{(R-d)(R+h)}{{R}^{2}}$ | D. | $\frac{(R-d)(R+h)^{2}}{{R}^{3}}$ |
分析 根据题意知,地球表面的重力加速度等于半径为R的球体在表面产生的加速度,深度为d的地球内部的重力加速度相当于半径为R-d的球体在其表面产生的重力加速度,根据地球质量分布均匀得到加速度的表达式,再根据半径关系求解深度为d处的重力加速度与地面重力加速度的比值.卫星绕地球做圆周运动时,运用万有引力提供向心力可以解出高度为h处的加速度,再求其比值
解答 解:令地球的密度为ρ,则在地球表面,重力和地球的万有引力大小相等,有:g=$\frac{GM}{{R}^{2}}$,
由于地球的质量为:M=$\frac{4}{3}π{R}^{3}ρ$,所以重力加速度的表达式可写成:g=$\frac{4}{3}πGρR$.
根据题意有,质量分布均匀的球壳对壳内物体的引力为零,固在深度为d的地球内部,受到地球的万有引力即为半径等于(R-d)的球体在其表面产生的万有引力,故井底的重力加速度g′=$\frac{4}{3}πGρ(R-d)$πGρ(R-d).
所以有$\frac{g′}{g}$=$\frac{R-d}{R}$.
根据万有引力提供向心力$\frac{GMm}{(R+h)^{2}}$=ma,“天宫一号”的加速度a=$\frac{GM}{(R+h)^{2}}$,
所以$\frac{a}{g}$=$\frac{{R}^{2}}{(R+h)^{2}}$,
所以$\frac{{g}^{′}}{a}$=$\frac{(R-d)(R+h)^{2}}{{R}^{3}}$,故D正确,A、B、C错误.
故选:D
点评 抓住在地球表面重力和万有引力相等,在地球内部,地球的重力和万有引力相等,要注意在地球内部距离地面d处所谓的地球的质量不是整个地球的质量而是半径为(R-d)的球体的质量m.


科目:高中物理 来源: 题型:选择题
| A. | 根据U=dE可知,在匀强电场中任意两点间的电势差与这两点间的距离成正比 | |
| B. | 可用P=I2R来计算电风扇正常工作时内阻的发热功率 | |
| C. | 由公式C=$\frac{Q}{U}$,电容器的电容由带电量Q的多少决定 | |
| D. | 由公式B=$\frac{F}{IL}$可知,磁场中某一点的磁感应强度跟F、I、L都有关 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,四个标有“11V、4.4W”的完全相同的灯泡,按如图所示分别接在理想变压器的原、副线圈上,且都正常发光.下列说法正确的是( )
如图所示,四个标有“11V、4.4W”的完全相同的灯泡,按如图所示分别接在理想变压器的原、副线圈上,且都正常发光.下列说法正确的是( )| A. | 变压器原、副线圈匝数之比为1:2 | B. | 灯泡L1两端电压为22V | ||
| C. | 交流电源两端电压为33 V | D. | 交流电源的输出功率为17.6 W |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 质量为m=2.0kg的物体,从竖直平面内高h=0.45m的光滑弧形轨道上的A点,无初速地沿轨道滑下,并进入水平轨道BC,如图所示.已知物体与水平轨道间的动摩擦因数μ=0.40,求:
质量为m=2.0kg的物体,从竖直平面内高h=0.45m的光滑弧形轨道上的A点,无初速地沿轨道滑下,并进入水平轨道BC,如图所示.已知物体与水平轨道间的动摩擦因数μ=0.40,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
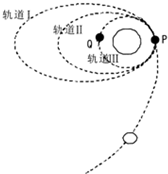 如图所示,嫦娥二号卫星进入地月转移轨道后,需经多次变轨才能最终进入距离月球表面100公里,周期为118分钟的工作轨道.下列有关嫦娥二号运动过程中说法正确的是( )
如图所示,嫦娥二号卫星进入地月转移轨道后,需经多次变轨才能最终进入距离月球表面100公里,周期为118分钟的工作轨道.下列有关嫦娥二号运动过程中说法正确的是( )| A. | 由轨道Ⅰ转移到轨道Ⅱ时在P点要加速 | |
| B. | 在轨道Ⅰ上的最大速度比在轨道Ⅱ上的最大速度大 | |
| C. | 在轨道Ⅲ上经过P点的向心加速度比在轨道Ⅰ上经过P点时小 | |
| D. | 在轨道Ⅲ的运动速度比月球的第一宇宙速度大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一个滑雪人与滑板的总质量m=75kg,以v0=2m/s的初速度沿长为75m的山坡匀加速下滑,山坡的倾角θ=37°,滑板与山坡的动摩擦因数为μ=0.1,已知sin37°=0.6,cos37°=0.8,g取10m/s2,不计空气阻力,求:
一个滑雪人与滑板的总质量m=75kg,以v0=2m/s的初速度沿长为75m的山坡匀加速下滑,山坡的倾角θ=37°,滑板与山坡的动摩擦因数为μ=0.1,已知sin37°=0.6,cos37°=0.8,g取10m/s2,不计空气阻力,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 伽利略开创了运用逻辑推理和实验相结合进行科学研究的方法 | |
| B. | 卡文迪许在利用扭秤实验装置测量万有引力常量时,应用了放大法 | |
| C. | 合力与分力、总电阻、交流电的有效值用的是“等效替代”的方法 | |
| D. | 电场强度是用比值法定义的,因而电场强度与电场力成正比,与试探电荷的电量成反比 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,一质量为M的斜面体B放在水平面上,在其斜面上放一质量为m的物体A,用一沿斜面向上的力F作用于物体A上,使其沿斜面匀速下滑,在物体A下滑的过程中,斜面体B静止不动,则地面对斜面体B的摩擦力Ff及支持力FN是( )
如图所示,一质量为M的斜面体B放在水平面上,在其斜面上放一质量为m的物体A,用一沿斜面向上的力F作用于物体A上,使其沿斜面匀速下滑,在物体A下滑的过程中,斜面体B静止不动,则地面对斜面体B的摩擦力Ff及支持力FN是( )| A. | Ff=0,FN=Mg+mg | B. | Ff向左,FN<Mg+mg | C. | Ff向右,FN<Mg+mg | D. | Ff向左,FN=Mg+mg |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com