在一条平直的公路上有甲、乙两车站,两车站相距s,今有一辆小车准备从甲站出发,并要求安全停靠乙站.已知小车加速时的加速度大小a1=4m/s2,小车减速时的加速度大小为a2=5m/s2,小车的最大允许速度为υm=20m/s请回答下列问题:
(1)若s=150m,小车从甲站到乙站最短时间为多少?
(2)若s=72m,小车从甲站到乙站最短时间为多少?
解:(1)当小车匀加速直线运动到最大速度的位移
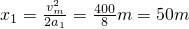
,匀加速运动的时间
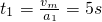
.
小车匀减速运动到零的位移
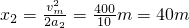
,匀减速直线运动的时间
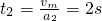
匀速运动的时间
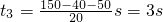
则最短时间t=5+2+3s=10s.
(2)设小车达到的最大速度为v,有
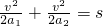
代入数据解得v=
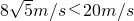
.
则运动的最短时间
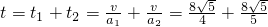
s=
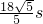
.
答:(1)若s=150m,小车从甲站到乙站最短时间为10s.
(2)若s=72m,小车从甲站到乙站最短时间为
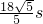
.
分析:当s=150m,小车先加速到最大速度后,匀速运动一段时间后再减速,运动时间最短.当s=72m时,小车先加速后减速,运动时间最短,结合位移关系,运用运动学公式求出最短的时间.
点评:解决本题的关键知道如何运动时运动时间最短,结合速度位移公式和位移时间公式以及速度时间公式进行求解.

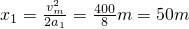 ,匀加速运动的时间
,匀加速运动的时间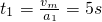 .
.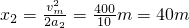 ,匀减速直线运动的时间
,匀减速直线运动的时间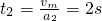
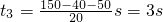
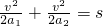
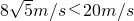 .
.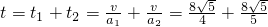 s=
s=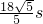 .
.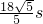 .
.
