
 宇宙中两颗相距较近的天体称为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动而不至因万有引力的作用吸引到一起.设双星的质量分别为m1和m2,两者相距L,求:
宇宙中两颗相距较近的天体称为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动而不至因万有引力的作用吸引到一起.设双星的质量分别为m1和m2,两者相距L,求:分析 (1)双星靠相互间的万有引力提供向心力,抓住角速度相等,向心力相等求出轨道半径之比;结合线速度与角速度的关系求出线速度之比.
(2)万有引力提供向心力,应用万有引力公式与牛顿第二定律可以求出角速度.
解答 解:(1)双星做圆周运动的角速度ω相等,万有引力提供向心力,由牛顿第二定律得:
G$\frac{{m}_{1}{m}_{2}}{{L}^{2}}$=m1ω2R1…①G$\frac{{m}_{1}{m}_{2}}{{L}^{2}}$=m2ω2R2…②
两星球半径之和等于两星间的距离:R1+R2=L,
解得:$\frac{{v}_{1}}{{v}_{2}}$=$\frac{{m}_{2}}{{m}_{1}}$,即它们的线速度之比等于质量的反比;
(2)由①式得:ω2=G$\frac{{m}_{2}}{{L}^{2}{R}_{1}}$=G$\frac{{m}_{2}}{{L}^{2}(L-{R}_{2})}$…③
由②式得:R2=G$\frac{{m}_{1}}{{L}^{2}{ω}^{2}}$…④
④式代入③式得:ω=$\sqrt{\frac{G({m}_{1}+{m}_{2})}{{L}^{3}}}$;
答:(1)它们的线速度大小之比为:m2:m1.
(2)它们角速度的表达式为:ω=$\sqrt{\frac{G({m}_{1}+{m}_{2})}{{L}^{3}}}$.
点评 本题考查了万有引力定律的应用,解决本题的关键掌握双星模型系统,知道它们靠相互间的万有引力提供向心力,向心力的大小相等,角速度的大小相等.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:选择题
 如图所示,物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧,物体B的质量为2m,因挡板P阻挡而静止在倾角为30°的光滑斜面上,物体A的质量为m,用手托着使弹簧处于原长,左边细绳伸直且与斜面保持平行,右边细绳竖直,A与地面的距离为h,放手后物体A下落,与地面即将接触时速度大小为v,此时物体B对挡板恰好无压力,针对以上叙述的运动过程,下列说法正确的是( )
如图所示,物体A、B通过细绳及轻质弹簧连接在轻滑轮两侧,物体B的质量为2m,因挡板P阻挡而静止在倾角为30°的光滑斜面上,物体A的质量为m,用手托着使弹簧处于原长,左边细绳伸直且与斜面保持平行,右边细绳竖直,A与地面的距离为h,放手后物体A下落,与地面即将接触时速度大小为v,此时物体B对挡板恰好无压力,针对以上叙述的运动过程,下列说法正确的是( )| A. | 物体A的机械能守恒 | |
| B. | A、B和弹簧组成的系统机械能不守恒 | |
| C. | 弹簧的最大弹性势能等于mgh-$\frac{1}{2}$mv2 | |
| D. | 此后物体B可能离开挡板沿斜面向上运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 加速度是物体增加的速度 | |
| B. | 加速度是描述物体速度变化的物理量 | |
| C. | 加速度是描述物体速度变化快慢的物理量 | |
| D. | 物体运动的加速度不变,物体运动的速度就一定不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图所示,一段横截面为正方形的玻璃棒,中间部分弯成四分之一圆弧形状,一细束单色光由MN端面的中点垂直射入,恰好能在弧面EF上发生全反射,然后垂直PQ端面射出.则该玻璃棒的折射率为$\sqrt{2}$,若将入射光向N端平移,当第一次射到弧面EF上时能(填“能”、“不能”或“无法确定能否”)发生全反射.
如图所示,一段横截面为正方形的玻璃棒,中间部分弯成四分之一圆弧形状,一细束单色光由MN端面的中点垂直射入,恰好能在弧面EF上发生全反射,然后垂直PQ端面射出.则该玻璃棒的折射率为$\sqrt{2}$,若将入射光向N端平移,当第一次射到弧面EF上时能(填“能”、“不能”或“无法确定能否”)发生全反射.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 伽利略的理想斜面实验反映了一个重要事实:如果忽略空气阻力和摩擦力,让小球从左边斜面上某一点滚下,必将冲上右边斜面的相同高度处,这说明:小球在运动过程中有一个物理量是不变的,这个物理量是( )
伽利略的理想斜面实验反映了一个重要事实:如果忽略空气阻力和摩擦力,让小球从左边斜面上某一点滚下,必将冲上右边斜面的相同高度处,这说明:小球在运动过程中有一个物理量是不变的,这个物理量是( )| A. | 机械能 | B. | 速度 | C. | 加速度 | D. | 弹力 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 它们的动能之比为Ek1:Ek2=1:6 | |
| B. | 它们的向心加速度之比为aA:aB=1:9 | |
| C. | 它们的向心力之比为FA:FB=1:18 | |
| D. | 它们的周期之比为TA:TB=3:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 若v0>$\sqrt{gH}$,两物体相遇时,B正在下降途中 | |
| B. | 若v0=$\sqrt{gH}$,两物体在地面相遇 | |
| C. | 若$\sqrt{gH}$>v0>$\sqrt{\frac{gH}{2}}$,两物体相遇时B物体正在空中下落 | |
| D. | 若v0=$\sqrt{\frac{gH}{2}}$,则两物体在地面相遇 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
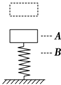 一物块从某一高度自由落下,落在竖立于地面的轻弹簧上.物块在A处开始与弹簧接触,到B处时物块速度为零,然后被弹回.下列说法正确的是( )
一物块从某一高度自由落下,落在竖立于地面的轻弹簧上.物块在A处开始与弹簧接触,到B处时物块速度为零,然后被弹回.下列说法正确的是( )| A. | 物块从A处下降到B处的过程中,速率不断减小 | |
| B. | 物块从B处上升到A处的过程中,速率不断增大 | |
| C. | 物块在B处时,所受合力为零 | |
| D. | 物块从A处下降到B处的过程中速率先增大,后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | b、c的线速度大小相等,且大于a的线速度 | |
| B. | b、c的向心加速度大小相等,且小于a的向心加速度 | |
| C. | b、c的角速度大小相等,且大于a的角速度 | |
| D. | c只要加速就可以追上b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com