

分析 (1)根据粒子只受到洛伦兹力作用下,做匀速圆周运动,结合周期公式,及牛顿第二定律与运动学公式,即可求解;
(2)根据圆周运动的半径公式,结合几何关系,及位移公式,即可求解.
解答 解:(1)只有磁场时,粒子在磁场中做匀速圆周运动,设周期为T,则有:
T=$\frac{2πm}{q{B}_{0}}$=2t0…①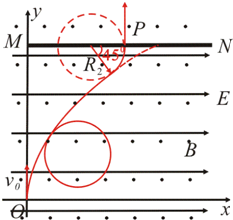
带电粒子在3nt0~(3n+1)t0(n=0,1,2…)时间段内只受电场力,且只有电场时粒子的运动连接起来才成为完整的类平抛运动,粒子在t=4t0时间内受电场力的运动时间t′=2t0.
设t=4t0时粒子速度v与v0成θ角,则有:vx=at′…②
$v=\sqrt{{v}_{0}^{2}+{v}_{x}^{2}}$…③
由牛顿第二定律,则有:a=$\frac{q{E}_{0}}{m}$…④
且tanθ=$\frac{{v}_{x}}{{v}_{0}}$…⑤
联立②③④⑤代入E0解得:v=$\sqrt{2}$v0,θ=45°…⑥
(2)若在0~6t0时间内,带电粒子垂直打在挡板MN上,则粒子一定是沿逆时针方向做匀速圆周运动时打在挡板MN上,故在4t0~6t0时间内打在挡板上,如图所示.轨道半径设为R2,则有:$qv{B}_{0}=m\frac{{v}^{2}}{{R}_{2}}$…⑦
由⑥式可知,粒子速度只需要偏转450角即可垂直打在到挡板上,故偏转时间为:
t″=$\frac{T}{8}$=$\frac{{t}_{0}}{4}$…⑧
粒子从原点O运动到P点所需时间为:t=4t0+t″=$\frac{17}{4}{t}_{0}$=4.25t0…⑨
P点横坐标为:x=x1+R2(1-cos45°)…⑩
纵坐标为:y=y1+R2sin45°…⑪
其中类平抛运动在t′=2t0时间内的位移我:x1=$\frac{1}{2}at{′}^{2}$…⑫
y1=v0t′…⑬
联立④⑦⑩⑪⑫⑬解得:x=$(1+\frac{1}{π}(\sqrt{2}-1)){v}_{0}{t}_{0}$,
y=(2+$\frac{1}{π}$)v0t0
则P点坐标为($(1+\frac{1}{π}(\sqrt{2}-1)){v}_{0}{t}_{0}$,(2+$\frac{1}{π}$)v0t0).
答:(1)则t=4t0时刻粒子的速度v大小$\sqrt{2}$v0;
(2)若在0-6t0时间内,带电粒子能垂直打在平行x轴放置的挡板MN上的P点,试求带电粒子打击挡板时的位置坐标P($(1+\frac{1}{π}(\sqrt{2}-1)){v}_{0}{t}_{0}$,(2+$\frac{1}{π}$)v0t0),及粒子从原点O运动到P的时间4.25t0
点评 考查带电粒子在复合场中的综合应用,掌握匀速圆周运动的周期与半径公式,同时运用牛顿第二定律与运动学公式,注意画出正确的运动轨迹图是解题的关键.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中物理 来源: 题型:解答题
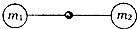 质量不计的硬杆长L=30cm,两端分别固定一个可以看成质点的小球,m1=0.6kg,m2=0.3kg将杆的中点固定子在光滑的水平轴上,并用力让装置静止在水平状态,如图所示,突然撤销外力,让两小球从静止开始在竖直面内转动,近似取重力加速度g=10m/s2,求:
质量不计的硬杆长L=30cm,两端分别固定一个可以看成质点的小球,m1=0.6kg,m2=0.3kg将杆的中点固定子在光滑的水平轴上,并用力让装置静止在水平状态,如图所示,突然撤销外力,让两小球从静止开始在竖直面内转动,近似取重力加速度g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,有一金属块垂直于表面C的匀强磁场中,磁场的磁感应强度为B,金属块的厚度为d,高度为h,当有稳定恒电流I平行平面C的方向通过时,由于磁场力的作用,金属块的上下两表面M、N间的电压为U,则金属块中单位体积内参与导电的自由电子数目为( )
如图所示,有一金属块垂直于表面C的匀强磁场中,磁场的磁感应强度为B,金属块的厚度为d,高度为h,当有稳定恒电流I平行平面C的方向通过时,由于磁场力的作用,金属块的上下两表面M、N间的电压为U,则金属块中单位体积内参与导电的自由电子数目为( )| A. | $\frac{BI}{edU}$ | B. | $\frac{BI}{ehU}$ | C. | $\frac{edU}{IB}$ | D. | $\frac{ehU}{IB}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 2013年6月,我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接.如图所示,已知“神舟十号”从捕获“天宫一号”到实现对接用时t,这段时间内组合体绕地球转过的角度为θ(此过程轨道不变,速度大小不变),地球半径为R,地球表面重力加速度为g,万有引力恒量G,不考虑地球自转;求:
2013年6月,我国成功实现目标飞行器“神舟十号”与轨道空间站“天宫一号”的对接.如图所示,已知“神舟十号”从捕获“天宫一号”到实现对接用时t,这段时间内组合体绕地球转过的角度为θ(此过程轨道不变,速度大小不变),地球半径为R,地球表面重力加速度为g,万有引力恒量G,不考虑地球自转;求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 计算如下情况中质量m=1kg的物体所受到的弧面弹力F的大小(g取10m/s2).
计算如下情况中质量m=1kg的物体所受到的弧面弹力F的大小(g取10m/s2).查看答案和解析>>
科目:高中物理 来源: 题型:多选题
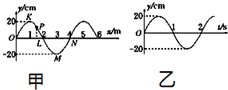 某横波在介质中沿x轴传播,图甲为t=0.25s时的波形图,图乙为P点(x=1.5m处的质点)的振动图象,那么下列说法正确的是( )
某横波在介质中沿x轴传播,图甲为t=0.25s时的波形图,图乙为P点(x=1.5m处的质点)的振动图象,那么下列说法正确的是( )| A. | 该波向右传播,波速为2m/s | |
| B. | 质点L与质点N的运动方向总相反 | |
| C. | t=0.25s时,质点M正处于平衡位置,并正在往正方向运动 | |
| D. | t=1.25s时,质点K向右运动了2m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com