
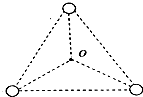
 由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )
由三颗星体构成的系统,忽略其他星体的对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在平面内做相同角速度的匀速圆周运动.如图,三颗星体的质量均为m,三角形的边长为a,万有引力常量为G,下列说法正确的是( )| A. | 每个星体受到向心力大小均为3$\frac{G{m}^{2}}{{a}^{2}}$ | |
| B. | 每个星体的角速度均为$\sqrt{\frac{3Gm}{{a}^{2}}}$ | |
| C. | 若a不变,m是原来的两倍,则周期是原来的$\frac{1}{2}$ | |
| D. | 若m不变,a是原来的4倍,则线速度是原来的$\frac{1}{2}$ |
分析 先写出任意两个星星之间的万有引力,求每一颗星星受到的合力,该合力提供它们的向心力.然后用R表达出它们的轨道半径,最后写出用周期和线速度表达的向心力的公式,整理即可的出结果.
解答 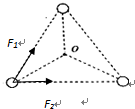 解:A、对任意一个星体,受力分析如图,有:
解:A、对任意一个星体,受力分析如图,有:
${F}_{1}^{\;}=G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}$,
${F}_{2}^{\;}=G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}$,
进行正交分解有:
${F}_{1x}^{\;}={F}_{1}^{\;}cos60°=\frac{1}{2}G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}$
${F}_{1y}^{\;}={F}_{1}^{\;}sin60°=\frac{\sqrt{3}}{2}G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}$
水平方向的合力为:${F}_{x}^{\;}={F}_{1x}^{\;}+{F}_{2}^{\;}=\frac{3}{2}G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}$
每个星体受到的向心力为:$F=\sqrt{{F}_{x}^{2}+{F}_{1y}^{2}}=\sqrt{3}G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}$,故A错误;
B、每个星体绕中心做匀速圆周运动的半径$r=\frac{\sqrt{3}a}{2}×\frac{2}{3}=\frac{\sqrt{3}a}{3}$,根据万有引力提供向心力有$\sqrt{3}G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}=m{ω}_{\;}^{2}\frac{\sqrt{3}}{3}a$,解得:$ω=\sqrt{\frac{3Gm}{{a}_{\;}^{2}}}$,故B正确;
C、对每个星体,根据万有引力提供向心力$\sqrt{3}G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}\frac{\sqrt{3}a}{3}$,解得$T=2π\sqrt{\frac{{a}_{\;}^{2}}{3Gm}}$,若a不变,m是原来的两倍,则周期是原来的$\frac{\sqrt{2}}{2}$,故C错误;
D、对每个星体,根据万有引力提供向心力$\sqrt{3}G\frac{{m}_{\;}^{2}}{{a}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{\frac{\sqrt{3}a}{3}}$,解得:$v=\sqrt{\frac{Gm}{a}}$,若m不变,a是原来的4倍,则线速度是原来的$\frac{1}{2}$,故D正确;
故选:BD
点评 解决该题首先要理解模型所提供的情景,然后能够列出合力提供向心力的公式,才能正确解答题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 3 m | B. | 6 m | C. | 12 m | D. | 9 m |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,是一种电子扩束装置的原理示意图.直角坐标系原点O处有一电子发射装置,可以不断朝xOy平面内x≥0区域任意方向发射电子,电子的速率均为v0,已知电子的电荷量为e、质量为m.在0≤x≤d的区域内分布着沿x轴负方向的匀强电场,场强大小E=$\frac{3m{{v}_{0}}^{2}}{2ed}$,在x>d区域内分布着足够大且垂直于xOy平面向外的匀强磁场,磁感应强度大小B=$\frac{4m{v}_{0}}{ed}$,ab为一块很大的平面感光板,在磁场内平行于y轴放置,电子打到板上后会在板上形成一条亮线.不计电子的重力和电子之间的相互作用.求:
如图所示,是一种电子扩束装置的原理示意图.直角坐标系原点O处有一电子发射装置,可以不断朝xOy平面内x≥0区域任意方向发射电子,电子的速率均为v0,已知电子的电荷量为e、质量为m.在0≤x≤d的区域内分布着沿x轴负方向的匀强电场,场强大小E=$\frac{3m{{v}_{0}}^{2}}{2ed}$,在x>d区域内分布着足够大且垂直于xOy平面向外的匀强磁场,磁感应强度大小B=$\frac{4m{v}_{0}}{ed}$,ab为一块很大的平面感光板,在磁场内平行于y轴放置,电子打到板上后会在板上形成一条亮线.不计电子的重力和电子之间的相互作用.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 方程式${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是重核裂变反应方程 | |
| B. | β衰变所释放的电子是原子核内的中子转化成质子时所产生的 | |
| C. | 核力是短程力,与核子间的距离有关,有时表现为引力,有时表现为斥力 | |
| D. | 原子核所含核子单独存在时的总质量等于该原子核的质量 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
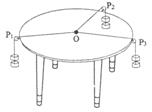 用如下的器材和方法可以验证“力的平行四边形定则“.在圆形桌子透明桌面上平铺一张白纸,在桌子边缘安装三个光滑的滑轮,其中,滑轮P1固定在桌子边,滑轮P2、P3可沿桌边移动.第一次实验中,步骤如下:
用如下的器材和方法可以验证“力的平行四边形定则“.在圆形桌子透明桌面上平铺一张白纸,在桌子边缘安装三个光滑的滑轮,其中,滑轮P1固定在桌子边,滑轮P2、P3可沿桌边移动.第一次实验中,步骤如下:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
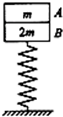 如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )
如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )| A. | 刚撤去外力F时,FN=$\frac{F+mg}{3}$ | B. | 弹簧弹力等于F时,FN=$\frac{F}{3}$ | ||
| C. | 当两物体速度最大时,FN=mg | D. | 当弹簧恢复原长时,FN=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com