
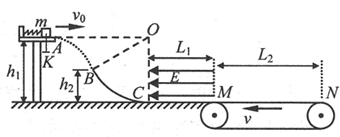
分析 (1)小球做平抛运动,求出平抛的竖直分速度,根据几何关系求出平抛的初速度,根据能量守恒定律求出弹簧的弹性势能
(2)小物块刚好没有从N端滑离传送带,到达N点时速度为零,从A到N根据能量守恒定律列式;
(3)求出物块在CM上摩擦产生的热量,再求出在传送带上摩擦产生的热量,最后求出总热量
解答 解:(1)打开锁扣K后,滑块从A到B做平抛运动,从B到C做圆周运动,设BC圆弧所对的圆心角为θ,
由几何关系有:$cosθ=\frac{{h}_{1}^{\;}-{h}_{2}^{\;}}{{h}_{1}^{\;}}=\frac{1.2-0.6}{1.2}=\frac{1}{2}$,得θ=60°
B点速度的竖直分量${v}_{By}^{2}=2g({h}_{1}^{\;}-{h}_{2}^{\;})$
代入数据解得:${v}_{By}^{\;}=\sqrt{2g({h}_{1}^{\;}-{h}_{2}^{\;})}=\sqrt{20×(1.2-0.6)}$=$2\sqrt{3}m/s$
将B点的速度分解如图所示,$tan60°=\frac{{v}_{By}^{\;}}{{v}_{0}^{\;}}$=$\frac{2\sqrt{3}}{{v}_{0}^{\;}}$
解得:${v}_{0}^{\;}=2m/s$
根据能量守恒:${E}_{p}^{\;}=\frac{1}{2}m{v}_{0}^{2}=\frac{1}{2}×1×{2}_{\;}^{2}=2J$
(2)小物块刚好没有从N端滑离传送带,到达N点时速度为零,从A到N
${E}_{p}^{\;}+mg{h}_{1}^{\;}=qE{L}_{1}^{\;}+μmg({L}_{1}^{\;}+{L}_{2}^{\;})$
代入数据解得:$E=1.0×1{0}_{\;}^{5}V/m$
(3)设小滑块第一次到达C点时的速度为${v}_{1}^{\;}$,第一次到达M点的速度为${v}_{2}^{\;}$
${E}_{p}^{\;}+mg{h}_{1}^{\;}=\frac{1}{2}m{v}_{1}^{2}$
解得:${v}_{1}^{\;}=2\sqrt{7}m/s$
$μmg{L}_{2}^{\;}=\frac{1}{2}m{v}_{2}^{2}$
解得:${v}_{2}^{\;}=4m/s$
小物块从传送带上返回先做匀加速,速度达到3m/s后做匀速运动,过M点再次进入匀强电场,假设能再次通过C点,设此时速度为${v}_{3}^{\;}$
$qE{L}_{1}^{\;}-μmg{L}_{1}^{\;}=\frac{1}{2}m{v}_{3}^{2}-\frac{1}{2}m{v}_{\;}^{2}$
解得:${v}_{3}^{\;}=\sqrt{1.8}m/s$
且$\frac{1}{2}m{v}_{3}^{2}=0.9J<mg{h}_{2}^{\;}=6J$
物块滑到圆轨道某处,又下滑经C点第三次进入电场,设物块停下时距C点的距离为x
$-(qE+μmg)x=0-\frac{1}{2}m{v}_{3}^{2}$
解得:x=0.18m
小物块在电场中摩擦发的热${Q}_{1}^{\;}=μmg(2{L}_{1}^{\;}+x)=10.32J$
${v}_{2}^{\;}=a{t}_{1}^{\;}$,得${t}_{1}^{\;}=1s$
$v=a{t}_{2}^{\;}$,得${t}_{2}^{\;}=0.75s$
小物块在传送带上发的热
${Q}_{2}^{\;}=μmg({L}_{2}^{\;}+v{t}_{1}^{\;})+μmg(v{t}_{2}^{\;}-\frac{v}{2}{t}_{2}^{\;})$=24.5J
总的发热:$Q={Q}_{1}^{\;}+{Q}_{2}^{\;}=34.82J$
答:(1)压缩的弹簧在被锁扣K锁住时所储存的弹性势能${E}_{p}^{\;}$为2J;
(2)匀强电场的场强大小E为$1.0×1{0}_{\;}^{5}V/m$;
(3)小物块从开始运动到最后静止在某点的整个运动过程中摩擦力产生的热量Q为34.82J.
点评 本题考查的是一道力电综合题,关键是分析清楚物块的运动过程,选择合适的规律解题,题目阅读量量大,有一定的难度.


科目:高中物理 来源: 题型:选择题
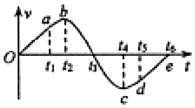 一个小孩在蹦床上做游戏,他从高处落到蹦床上后又被弹起到原高度.小孩从开始下落到弹回的整个过程中,他的速度随时间变化的图象如图所示,图中Oa段和de段为直线,b,c对应速度的最大值,则根据此图象可知( )
一个小孩在蹦床上做游戏,他从高处落到蹦床上后又被弹起到原高度.小孩从开始下落到弹回的整个过程中,他的速度随时间变化的图象如图所示,图中Oa段和de段为直线,b,c对应速度的最大值,则根据此图象可知( )| A. | 在t1-t2过程中,小孩处于失重状态 | B. | 在t2-t3过程中,小孩处于失重状态 | ||
| C. | 在t2时刻蹦床形变最大 | D. | 在t4时刻小孩离开蹦床 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,轻质弹簧的两端均在5N的拉力作用下,弹簧伸长了10cm(在弹性限度内).下列说法正确的是( )
如图所示,轻质弹簧的两端均在5N的拉力作用下,弹簧伸长了10cm(在弹性限度内).下列说法正确的是( )| A. | 此时弹簧所受的合力为零 | B. | 此时弹簧的弹力为10 N | ||
| C. | 该弹簧的劲度系数为50N/m | D. | 该弹簧的劲度系数为100 N/m |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,AB为竖直墙壁,A点和P点在同一水平面上相距为 L,将一质量为m,电量为q的带正电小球从P点以水平速度v向A抛出,结果打在墙上的C处.如果在空间加上方向竖直向下的匀强电场,将小球从P点以水平速度2v向A抛出,也正好打在墙上的C点.(已知重力加速度g)求:
如图所示,AB为竖直墙壁,A点和P点在同一水平面上相距为 L,将一质量为m,电量为q的带正电小球从P点以水平速度v向A抛出,结果打在墙上的C处.如果在空间加上方向竖直向下的匀强电场,将小球从P点以水平速度2v向A抛出,也正好打在墙上的C点.(已知重力加速度g)求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
| 速度(km/h) | 反应距离(m) | 制动距离(m) | 刹车距离(m) |
| 40 | 7 | 8 | 15 |
| 50 | 9 | 13 | 22 |
| 60 | 11 | 20 | 31 |
| 80 | 15 | 34 | 49 |
| 100 | 19 | 54 | 73 |
| 速度(km/h) | 反应距离(m) | 制动距离(m) | 刹车距离(m) |
| 40 | 8 | 8 | 16 |
| 50 | 10 | 13 | 23 |
| 60 | 12 | 20 | 32 |
| 80 | 16 | 34 | 50 |
| 100 | 20 | 54 | 74 |
| 速度(km/h) | 反应距离(m) | 制动距离(m) | 刹车距离(m) |
| 40 | 7 | 8 | 15 |
| 50 | 9 | 13 | 22 |
| 60 | 11 | 20 | 31 |
| 80 | 15 | 34 | 49 |
| 100 | 19 | 54 | 73 |
| 速度(km/h) | 反应距离(m) | 制动距离(m) | 刹车距离(m) |
| 40 | 7 | 11 | 18 |
| 50 | 9 | 17 | 26 |
| 60 | 11 | 25 | 36 |
| 80 | 15 | 44 | 59 |
| 100 | 19 | 69 | 88 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 用“伏安法”测定电源的电动势和内阻,所给器材如图甲所示,已知电源的内阻很小.
用“伏安法”测定电源的电动势和内阻,所给器材如图甲所示,已知电源的内阻很小.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com