
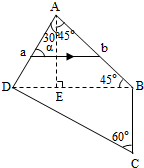
 ��ͼ��ʾ�������⾵ABCD���Կ������ɡ�ADE����ABE����BCD����ֱ�����⾵��ɣ�һ��Ƶ��f=5.3��1014Hz�ĵ�ɫ������AD�����䣬���⾵�е����������ͼ��ab��ʾ��ab��AD��ļнǦ�=60�㣬��֪��������е��ٶ�c=3��108m/s��������������n=1.5����
��ͼ��ʾ�������⾵ABCD���Կ������ɡ�ADE����ABE����BCD����ֱ�����⾵��ɣ�һ��Ƶ��f=5.3��1014Hz�ĵ�ɫ������AD�����䣬���⾵�е����������ͼ��ab��ʾ��ab��AD��ļнǦ�=60�㣬��֪��������е��ٶ�c=3��108m/s��������������n=1.5�������� ��1�����ݹ�����䶨�ɣ���ϼ��ι�ϵ��������⣻
��2������n=$\frac{c}{v}$����ù��ڽ����д����ٶȣ��ٸ���v=��f����ò��������������������ٽ�ǵĹ�ϵ������·���棬������⣮
��� �⣺��1�������AD�������ǣ�����Ƿֱ�Ϊi��r�����У�r=30��
���ݹ�����䶨�ɣ�n=$\frac{sini}{sinr}$��
��ã�sini=nsinr=1.5��sin30��=0.75��
��2������n=$\frac{c}{v}$����ã�v=$\frac{c}{n}$=$\frac{3��1{0}^{8}}{1.5}$=2��108m/s��
��v=��f����ã�$��=\frac{v}{f}$=$\frac{2��1{0}^{8}}{5.3��1{0}^{14}}$m=3.77��10-7m��
��sin45��=$\frac{\sqrt{2}}{2}$$��\frac{2}{3}$����֪������AB���Ϸ���ȫ���䣬��CD���ϵ������Ϊ30�㣬
�ʸ��ݹ�·����ԭ������֪�����CD������ij���ǵ�����ֵΪ0.75��
�𣺣�1������������ߵ�����ǵ�����ֵ0.75��
��2�������⾵�еIJ�������CD������ij���ǵ�����ֵ0.75��
���� �����е����ߴӲ����������ʱ��Ҫ������������ٽ�ǵĹ�ϵ���ж��ܷ���ȫ���䣬������ǿ��Ը��ݼ���֪ʶ�����ͬʱ���չ�����䶨��Ӧ�ã�


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��������ij��ٶ���ȣ������ǵ�����о������ | |
| B�� | ��������ij��ٶ���ȣ�������С������о���� | |
| C�� | ��������ij�������ȣ�������С������о���� | |
| D�� | ��������ij�������ȣ������ǵ�����о������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��ϸ��һ��ϵ������M=0.6kg������A��ֹ��ˮƽת̨�ϣ���һ��ͨ������С����O��������m=0.3kg�����壮A�뻬��O�ľ���Ϊ0.2m������ˮƽ������Ħ����Ϊ2N��ΪʹB���־�ֹ״̬��ˮƽת̨��Բ���˶��Ľ��ٶȦ�Ӧ��ʲô��Χ�ڣ���gȡ10m/s2��
��ͼ��ʾ��ϸ��һ��ϵ������M=0.6kg������A��ֹ��ˮƽת̨�ϣ���һ��ͨ������С����O��������m=0.3kg�����壮A�뻬��O�ľ���Ϊ0.2m������ˮƽ������Ħ����Ϊ2N��ΪʹB���־�ֹ״̬��ˮƽת̨��Բ���˶��Ľ��ٶȦ�Ӧ��ʲô��Χ�ڣ���gȡ10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���ռ����ˮƽ���ҵ���ǿ�糡������ֱƽ���Ͻ���ƽ��ֱ�����꣬������ƽ��ĵ�һ�����ڹ̶���Ե�⻬�İ뾶ΪR��$\frac{1}{4}$Բ�ܹ����������������������ϣ�����Ϊm�Ĵ������С��ӹ���϶��ɾ�ֹ��ʼ���£���֪����Ϊ�糡����2������
��ͼ��ʾ���ռ����ˮƽ���ҵ���ǿ�糡������ֱƽ���Ͻ���ƽ��ֱ�����꣬������ƽ��ĵ�һ�����ڹ̶���Ե�⻬�İ뾶ΪR��$\frac{1}{4}$Բ�ܹ����������������������ϣ�����Ϊm�Ĵ������С��ӹ���϶��ɾ�ֹ��ʼ���£���֪����Ϊ�糡����2�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ѹ���Ǹı佻�����ѹ���豸�������ܾ��е����ԣ���������ܵ�����������Ϊ�㣬����������Ϊ�������������������븺�ص���R������ӵ���ѹ������Ȧ�����ˣ���ѹ����ԭ��Ȧ�д���һ����ɺ��Բ��Ƶĵ���������ѹ��ԭ������Ȧ������Ϊn1��n2��ԭ��Ȧa��b�����������ҽ����������ͼ��ʾ��������
��ѹ���Ǹı佻�����ѹ���豸�������ܾ��е����ԣ���������ܵ�����������Ϊ�㣬����������Ϊ�������������������븺�ص���R������ӵ���ѹ������Ȧ�����ˣ���ѹ����ԭ��Ȧ�д���һ����ɺ��Բ��Ƶĵ���������ѹ��ԭ������Ȧ������Ϊn1��n2��ԭ��Ȧa��b�����������ҽ����������ͼ��ʾ��������| A�� | a��b�˺�c��d�˵�ѹ֮��ΪUab��Ucd=n1��n2 | |
| B�� | �����ص���R����ֵ����������ʾ����С | |
| C�� | c��d���ѹUcd���渺�ص���ı仯���仯 | |
| D�� | �������ܱ��������������ܷ�����·�������������ʾ��������Ϊԭ����$\sqrt{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�����й⻬С������ϸ����ˮƽ�˵�����A��B�ϣ�������ˮƽ�����˶�ʱ��С��ǡ������A�˵����·�����˱�����Ծ�ֹ����֪С������Ϊm���������ٶ�Ϊg�����з�����ȷ���ǣ�������
��ͼ��ʾ�����й⻬С������ϸ����ˮƽ�˵�����A��B�ϣ�������ˮƽ�����˶�ʱ��С��ǡ������A�˵����·�����˱�����Ծ�ֹ����֪С������Ϊm���������ٶ�Ϊg�����з�����ȷ���ǣ�������| A�� | �˿����������˶� | |
| B�� | ϸ�ߵ��������ܵ���mg | |
| C�� | ��һ�����������ٶȴ���g���ȼ����˶� | |
| D�� | �˿������������ٶ�С��g���ȼ����˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ������Ĥ��������ӵĴ�С��ʵ�����������ֱ�����ڴ��������������Ӧ����Ĥ����� | |
| B�� | һ������������������������������£�ѹǿp������ѧ�¶�T������ | |
| C�� | ������ӵ�ƽ������Խ�������ѹǿ��Խ�� | |
| D�� | �������ʸ���ͬ�Ե�һ���ǷǾ��� | |
| E�� | Һ��ı�������������Һ����Ӽ������������ | |
| F�� | ����Һ���Ϸ���������������䣬�����¶ȣ���ﵽ��̬ƽ���ñ����������������ܶ�����ѹǿҲ���� | |
| G�� | ��һС�������Բ���ڱ����ع�����С����˶��ǿ������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����ʯͷ�����Ӳ������ʯͷ�Լ��������������ڼ�����ʯͷ�������� | |
| B�� | ������ʯͷ����������ʯͷ�Լ�������������һ��ƽ��������С��ȡ������෴ | |
| C�� | ������ʯͷ����������ʯͷ�Լ�����������������ͬ����������� | |
| D�� | ������ʯͷ����������ʯͷ�Լ�������������С��ȣ�������������ʹ�������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 С����б�����ȼ���ֱ���˶�����Aλ�ÿ�ʼ��ʱ���������ʱ��t�ڼ�¼��С��λ����ͼ��d1��d2��d3�ֱ�Ϊλ��B��C��D��A�ľ��룮������
С����б�����ȼ���ֱ���˶�����Aλ�ÿ�ʼ��ʱ���������ʱ��t�ڼ�¼��С��λ����ͼ��d1��d2��d3�ֱ�Ϊλ��B��C��D��A�ľ��룮������| A�� | ��d3-d2��=��d2-d1�� | |
| B�� | С����Bʱ���ٶ�Ϊ$\frac{{��{d_2}-{d_1}��}}{2t}$ | |
| C�� | С����Cʱ���ٶ�Ϊ$\frac{{��{d_3}\right.-\left.{d_1}��}}{2t}$ | |
| D�� | С���˶��ļ��ٶ�Ϊ$\frac{{��{d_3}\right.-\left.{d_2}��}}{{4{t^2}}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com