
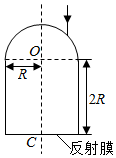
 如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜.有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R.已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射).求该玻璃的折射率.
如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜.有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R.已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射).求该玻璃的折射率. 分析 根据题意和光的折射规律画出光路图,由几何关系确定入射角的正弦值与折射角的正弦值,再由折射定律求玻璃的折射率;
解答 解:由题意,结合光路的对称性与光路可逆可知,与入射光相对于OC轴对称的出射光线一定与入射光线平行,所以从半球面射入的光线经折射后,将在圆柱体底面中心C点反射,如图:
设光线在半球处的入射角为i,折射光线的折射角为r,则: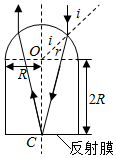
sini=nsinr…①
由正弦定理得:$\frac{sinr}{2R}=\frac{sin(i-r)}{R}$…②
由几何关系可知,入射点的法线与OC之间的夹角也等于i,该光线与OC之间的距离:L=0.6R
则:sini=$\frac{L}{R}=\frac{0.6R}{R}=0.6$…③
由②③得:sinr=$\frac{6}{\sqrt{205}}$
由①③④得:n=$\sqrt{2.05}$≈1.43
答:该玻璃的折射率为1.43.
点评 本题是几何光学问题,其基础是作出光路图,根据几何知识确定折射角是关键,结合折射定律求解.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:多选题
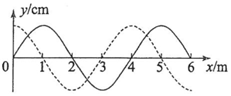 如图,一列简谐横波沿x轴正方向传播,实线为t=0时的波形图,虚线为t=0.5s时的波形图.已知该简谐波的周期大于0.5s.关于该简谐波,下列说法正确的是( )
如图,一列简谐横波沿x轴正方向传播,实线为t=0时的波形图,虚线为t=0.5s时的波形图.已知该简谐波的周期大于0.5s.关于该简谐波,下列说法正确的是( )| A. | 波长为2 m | |
| B. | 波速为6 m/s | |
| C. | 频率为1.5Hz | |
| D. | t=1s时,x=1m处的质点处于波峰 | |
| E. | t=2s时,x=2m处的质点经过平衡位置 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 该星球上的第一宇宙速度为$\frac{\sqrt{3gR}}{3}$ | B. | 该星球上的第二宇宙速度为$\frac{\sqrt{gR}}{3}$ | ||
| C. | 该星球的平均密度为$\frac{ρ}{2}$ | D. | 该星球的质量为$\frac{8π{R}^{3}ρ}{81}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
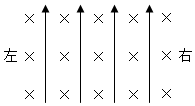 如图,空间某区域存在匀强电场和匀强磁场,电场方向竖直向上(与纸面平行),磁场方向垂直于纸面向里.三个带正电的微粒a,b,c电荷量相等,质量分别为ma,mb,mc.已知在该区域内,a在纸面内做匀速圆周运动,b在纸面内向右做匀速直线运动,c在纸面内向左做匀速直线运动.下列选项正确的是( )
如图,空间某区域存在匀强电场和匀强磁场,电场方向竖直向上(与纸面平行),磁场方向垂直于纸面向里.三个带正电的微粒a,b,c电荷量相等,质量分别为ma,mb,mc.已知在该区域内,a在纸面内做匀速圆周运动,b在纸面内向右做匀速直线运动,c在纸面内向左做匀速直线运动.下列选项正确的是( )| A. | ma>mb>mc | B. | mb>ma>mc | C. | mc>ma>mb | D. | mc>mb>ma |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
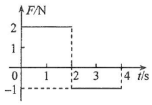 一质量为2kg的物块在合外力F的作用下从静止开始沿直线运动.F随时间t变化的图线如图所示,则( )
一质量为2kg的物块在合外力F的作用下从静止开始沿直线运动.F随时间t变化的图线如图所示,则( )| A. | t=1s时物块的速率为1m/s | B. | t=2s时物块的动量大小为4kg•m/s | ||
| C. | t=3s时物块的动量大小为5kg•m/s | D. | t=4s时物块的速度为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 我国自主研发制造的国际热核聚变核心部件在国际上率先通过权威机构认证,这是我国对国际热核聚变项目的重大贡献.下列核反应方程中属于聚变反应的是( )
我国自主研发制造的国际热核聚变核心部件在国际上率先通过权威机构认证,这是我国对国际热核聚变项目的重大贡献.下列核反应方程中属于聚变反应的是( )| A. | ${\;}_{1}^{2}H{+}_{1}^{3}H$→${\;}_{2}^{4}He{+}_{0}^{1}n$ | |
| B. | ${\;}_{7}^{14}{N+}_{2}^{4}He$→${\;}_{8}^{17}O{+}_{1}^{1}H$ | |
| C. | ${\;}_{2}^{4}He{+}_{13}^{27}Al$→${\;}_{15}^{30}P$+${\;}_{0}^{1}n$ | |
| D. | ${\;}_{92}^{235}U{+}_{0}^{1}n$→${\;}_{56}^{144}Ba$+${\;}_{36}^{89}Kr$+3${\;}_{0}^{1}n$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
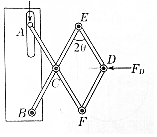 如图所示“拉链”机构,A可在竖槽中滑动,B、C、D、E、F为铰接,且AC=BC=EC=FC=ED=FD.在D处作用水平力FD,为保持机构平衡,在A处需施多大的竖直向下力T?
如图所示“拉链”机构,A可在竖槽中滑动,B、C、D、E、F为铰接,且AC=BC=EC=FC=ED=FD.在D处作用水平力FD,为保持机构平衡,在A处需施多大的竖直向下力T?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示为氢原子的能级结构示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外辐射出光子,用这些光子照射逸出功为2.49eV的金属钠,下列说法不正确的是( )
如图所示为氢原子的能级结构示意图,一群氢原子处于n=3的激发态,在向较低能级跃迁的过程中向外辐射出光子,用这些光子照射逸出功为2.49eV的金属钠,下列说法不正确的是( )| A. | 这群氢原子能辐射出三种不同频率的光,其中从n=3能级跃迁到n=2能级所发出的光波长最长 | |
| B. | 这群氢原子在辐射光子的过程中电子绕核运动的动能减小,电势能增大 | |
| C. | 能发生光电效应的光有两种 | |
| D. | 金属钠表面所发出的光电子的最大初动能是9.60 eV |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com