
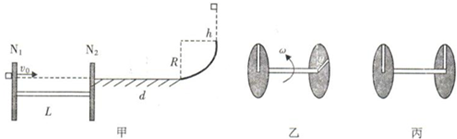
分析 (1)物块在两盘之间做匀速运动,合力为零,受到的恒力和重力平衡,即可由平衡条件求出恒力的大小.
(2)根据周期性和圆周运动的角速度公式,即可求出薄盘转动的角速度ω;
(3)由动能定理,选取物块向最高点运动的过程中,从而求得克服摩擦力做功,当返回时,再运用动能定理,因克服滑动摩擦力做功变小,进而可求得回到圆盘时的速度大小,从而求解.
解答 解:(1)由题意可知,物块在两盘间做匀速运动,滑块受到的恒力F和重力平衡,则有:
F=mg
代入数据解得:F=10N;
(2)根据运动学公式知,物块通过两盘的时间为:t=$\frac{L}{{v}_{0}}$=$\frac{1}{4}$=0.25s;
由角速度公式ω=$\frac{θ}{t}$,则有:ω=$\frac{2kπ+\frac{π}{3}}{t}$=(8kπ+$\frac{4}{3}$π )rad/s,k=0、1、2…
(3)小球向最高点运动的过程中,经过四分之一圆弧克服摩擦力做功为W;由动能定理得:
-W-μmgd-mg(R+h)=0-$\frac{1}{2}m{v}_{0}^{2}$
代入数据解得:W=2J;
若能到达N2,且到达时的速度大小为v,W′为返回时过四分之一圆弧克服摩擦力做功,由动能定理有:
mg(R+h)-μmgd-W′=$\frac{1}{2}$mv2,
因W′<2J,则有:v>0,因此能再次通过两狭缝.
答:(1)物块在两盘间受到的竖直向上恒力F的大小是10N.
(2)要使物块能通过两狭缝,薄盘转动的角速度ω为:(8kπ+$\frac{4}{3}$π )rad/s,k=0、1、2….
(3)物块返回后能再次通过两狭缝.
点评 本题是动能定理和圆周运动运动学公式的综合,关键是抓住圆周运动的周期性得到角速度的表达式,要注意球来回经过圆弧滑动摩擦力做功是不同的.


科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 义乌市“公共自行车”的投放,不仅为市民提供了一种低碳环保的出行方式,而且还缓解了交通堵塞.高中生小明骑自行车以5m/s的速度沿平直公路匀速前行,若骑行过程中所受阻力恒为车和人总重的0.02倍,那么小明骑车做功的平均功率最接近于( )
义乌市“公共自行车”的投放,不仅为市民提供了一种低碳环保的出行方式,而且还缓解了交通堵塞.高中生小明骑自行车以5m/s的速度沿平直公路匀速前行,若骑行过程中所受阻力恒为车和人总重的0.02倍,那么小明骑车做功的平均功率最接近于( )| A. | 10W | B. | 100W | C. | 1kW | D. | 10kW |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 匀速圆周运动 | B. | 变速圆周运动 | C. | 变加速直线运动 | D. | 匀变速曲线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
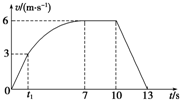 某探究性学习小组对一辆自制遥控车的性能进行研究.他们让这量小车在水平地面上由静止开始运动,并将小车运动的全过程记录下来,通过数据处理得到如图所示的v-t图象,已知小车在0~t1时间内做匀加速直线运动,t1~10s时间内小车牵引力的功率保持不变,7s末到达最大速度,在10s末停止遥控让小车自由滑行,小车质量m=0.5kg,整个过程中小车受到的阻力f大小不变.则以下说法正确的是( )
某探究性学习小组对一辆自制遥控车的性能进行研究.他们让这量小车在水平地面上由静止开始运动,并将小车运动的全过程记录下来,通过数据处理得到如图所示的v-t图象,已知小车在0~t1时间内做匀加速直线运动,t1~10s时间内小车牵引力的功率保持不变,7s末到达最大速度,在10s末停止遥控让小车自由滑行,小车质量m=0.5kg,整个过程中小车受到的阻力f大小不变.则以下说法正确的是( )| A. | 小车匀加速直线运动时牵引力大小为3N | |
| B. | 小车匀加速直线运动的时间t1=2s | |
| C. | 小车所受阻力f的大小为2N | |
| D. | t1~10s内小车牵引力的功率P为6W |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
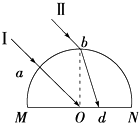 半径为R的半圆柱形玻璃砖的截面如图所示,O为圆心,光线Ⅰ沿半径方向从a点射入玻璃砖后,恰好在O点发生全反射,另一条光线Ⅱ平行于光线Ⅰ从最高点b射入玻璃砖后,在底边MN上的d点射出.若测得Od=$\frac{R}{3}$,求该玻璃砖的折射率.
半径为R的半圆柱形玻璃砖的截面如图所示,O为圆心,光线Ⅰ沿半径方向从a点射入玻璃砖后,恰好在O点发生全反射,另一条光线Ⅱ平行于光线Ⅰ从最高点b射入玻璃砖后,在底边MN上的d点射出.若测得Od=$\frac{R}{3}$,求该玻璃砖的折射率.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,从A点以v0的初速度抛出一个小球,在离A点水平距离为s处有一堵高度为h的墙BC,要求小球能越过B点,问小球以怎样的角度抛出,才能使v0最小?
如图所示,从A点以v0的初速度抛出一个小球,在离A点水平距离为s处有一堵高度为h的墙BC,要求小球能越过B点,问小球以怎样的角度抛出,才能使v0最小?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com