
| A. | 卫星的质量 | B. | 卫星的公转周期 | ||
| C. | 卫星的自转周期 | D. | 卫星绕木星的线速度 |
分析 卫星绕木星作圆周运动,根据万有引力提供向心力,列出等式分析.
解答 解:设卫星的质量为m,轨道半径为r,公转周期为T,线速度为v,木星的质量为M.
根据万有引力等于向心力,得:
G$\frac{Mm}{{r}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}r$
得:M=$\frac{4π{r}^{3}}{G{T}^{2}}$…①
由v=$\frac{2πr}{T}$,得:r=$\frac{vT}{2π}$…②
可知,若已知卫星的公转周期和线速度,由②式可求得轨道半径r,由①式求出木星的质量M,故BD正确,AC错误.
故选:BD.
点评 知道环绕天体的公转周期和半径,可求出的是中心天体的质量,只是常用的思路,要能熟练运用.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 灰尘的自然堆积 | |
| B. | 玻璃有较强的吸附灰尘的能力 | |
| C. | 电视机工作时,屏表面温度较高而吸附灰尘 | |
| D. | 电视机工作时,屏表面有静电而吸附灰尘 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
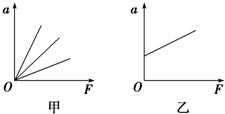 在探究影响加速度的因素的实验中,作出了如图所示的甲、乙两图象,图甲中三线表示实验中小车和砝码的总质量不同.图乙中图线不过原点的原因是由于长木板的倾角过大.
在探究影响加速度的因素的实验中,作出了如图所示的甲、乙两图象,图甲中三线表示实验中小车和砝码的总质量不同.图乙中图线不过原点的原因是由于长木板的倾角过大.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | F=0 | B. | $F=m\frac{R_0^2a}{{{{({R_0}+h)}^2}}}$ | ||
| C. | $F=m\root{3}{{a{r^2}ω_0^4}}$ | D. | $F=m\frac{r^2}{{{R_0}+h}}a$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 某同学利用数码相机连拍功能记录运动会上女子跳水比赛中运动员在10m跳台跳水的全过程.所拍摄的第一张照片恰为她们起跳的瞬间,第五张如图甲,该同学认为这时她们处在最高点,第二十一张如图乙,她们正好身体竖直、双手刚刚触及水面,查阅资料得知相机拍摄两张照片间隔时间T=0.1s(忽略相机曝光时间),设起跳时重心离台面及触水时重心离水面的距离相等,由以上材料:(g=10m/s2)
某同学利用数码相机连拍功能记录运动会上女子跳水比赛中运动员在10m跳台跳水的全过程.所拍摄的第一张照片恰为她们起跳的瞬间,第五张如图甲,该同学认为这时她们处在最高点,第二十一张如图乙,她们正好身体竖直、双手刚刚触及水面,查阅资料得知相机拍摄两张照片间隔时间T=0.1s(忽略相机曝光时间),设起跳时重心离台面及触水时重心离水面的距离相等,由以上材料:(g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
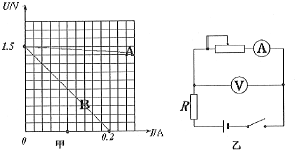 在测电源电动势和内阻实验中,由于电源内阻较小,电压表示数变化不明显,作出的U-I图象如图甲中A所示,这对数据处理的结果将引入较大误差,为了解决此问题,某同学在电路中串联了一定电阻R=6.8Ω(如图乙),作出的U-I图象如图甲中B所示,则此电源的电动势大小为1.5V,内阻为0.5Ω.
在测电源电动势和内阻实验中,由于电源内阻较小,电压表示数变化不明显,作出的U-I图象如图甲中A所示,这对数据处理的结果将引入较大误差,为了解决此问题,某同学在电路中串联了一定电阻R=6.8Ω(如图乙),作出的U-I图象如图甲中B所示,则此电源的电动势大小为1.5V,内阻为0.5Ω.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com